Tháng: Tháng Một 2021

Số Fibonacci và tỉ lệ vàng Ф có thể quan sát thấy ở vạn vật trong vũ trụ, từ vi mô nhất cho tới vĩ mô nhất, từ các nguyên tử cho tới các dải thiên hà, từ động vật tới thực vật và khoáng vật.

Dãy số Fibonacci và Tỉ lệ vàng (Ф)

Dãy số Fibonacci là dãy số bắt đầu bởi số 0 và số 1, các số sau mỗi số bằng tổng của 2 số liền trước nó. Các số đầu tiên của dãy Fibonacci là:

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, …

Nếu chúng ta lấy tỉ số của 2 số liên tiếp trong dãy Fibonacci thì sẽ được dãy số sau:

1/1 = 1 2/1 = 2 3/2 = 1,5 5/3 = 1,666… 8/5 = 1,6 13/8 = 1,625 21/13 = 1,61538…

Đồ thị biểu diễn cho dễ hình dung :

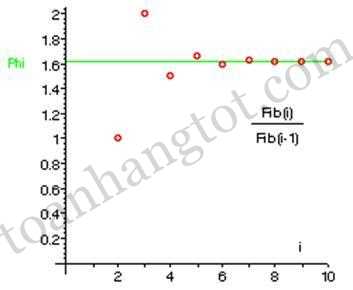
Tỉ số này sẽ tiến dần đến một giá trị mà ta hay gọi là Tỉ lệ Thần thánh hay tỉ lệ vàng: Ф ≈ 1,618

Một con số liên quan chặt chẽ với Ф là 1/Ф ≈ 0,618. Nghịch đảo của Ф nhỏ hơn nó đúng 1 đơn vị.

Số Fibonacci và Tỉ lệ vàng Ф có thể quan sát thấy ở vạn vật trong vũ trụ, từ vi mô nhất cho tới vĩ mô nhất, từ các nguyên tử cho tới các dải thiên hà, từ động vật tới thực vật và khoáng vật.

Bởi thực vật sống xung quanh con người rất nhiều, cho nên người ta dễ quan sát thấy Fibonacci ở cây cỏ thực vật nhất.

1. Ф và những bông hoa

Ở rất nhiều loài cây, số lượng cánh hoa là một số Fibonacci :

3 cánh	Hoa loa kèn, hoa Iris
5 cánh	Hoa dâm bụt, hoa cẩm chướng, hoa hồng dại, hoa phi yến, hoa sứ, hoa đào…
8 cánh	Phi yến
13 cánh	Cúc vạn thọ, cỏ lưỡi chó, một số loài cúc
21 cánh	Cúc tây, rau diếp xoăn
34, 55, 89 cánh	Một số loài Cúc, hoa mã đề

Hoa cẩm chướng

Hoa loa kèn mặc dù trông có vẻ 6 cánh nhưng thực ra chỉ 3 cánh, 3 cánh dưới là lá đài hoa

Một số loài hoa có số cánh hoa rất chính xác và không đổi, ví dụ như hoa sứ, nhưng các loài khác có số cánh hoa thay đổi rất gần với những con số trên – và số cánh hoa trung bình của mỗi loài là một số Fibonacci.

Ví dụ như dưới đây là loài hoa passion nhìn từ trước và sau :

Nhìn từ trước: 2 lớp cánh hoa bọc lấy dãy nhị hoa xanh trắng (không rõ số lượng), ở giữa là 5 nhị màu xanh, trên cùng ở giữa là 3 lá noãn màu nâu đậm.

Nhìn từ sau: ngoài cùng 3 lá đài, rồi đến 5 cánh hoa giữa, rồi đến năm cánh hoa trong nhạt màu hơn

2. Ф và nhị hoa

Số Fibonacci còn xuất hiện trong cách sắp xếp của nhị hoa. Trong ảnh dưới là phần nhị của một bông hoa cúc (Echinacea purpura).

Các phần tử nằm trên nhị hoa được sắp xếp nằm trên đồng thời vài hệ thống đường xoắn ốc, về phía trái và phải. Ở phần rìa tấm ảnh, nếu đếm số đường xoắn phải hướng ra ngoài ta sẽ được 55 đường xoắn ốc. Ở hệ thống kia ta đếm được 34 xoắn ốc. 34 và 55 là hai con số liền nhau trong dãy Fibonacci.

Dưới đây là nhị hoa hướng dương, với cách sắp xếp giống hệt như vậy :

Còn đây là một bông hướng dương lớn hơn, với các hệ thống xoắn ốc gồm 55 và 89 đường. Cả 55 và 89 đều là 2 số liền nhau trong dãy Fibonacci :

Điều tương tự cũng xảy ra ở nhị hoa nhiều loài hoa khác trong tự nhiên. Số đường xoắn ốc của các hệ thống đường xoắn ốc khác nhau của mỗi bông hoa thường xuyên là những con số thuộc dãy số Fibonacci (hoặc thuộc dãy họ Fibonacci).

Các nhị hoa lớn có thể có nhiều hệ thống đường xoắn ốc khác nhau

3. Ф và những quả thông

Quả thông có những đường xoắn ốc tuân theo dãy số Phibonacci khá rõ.

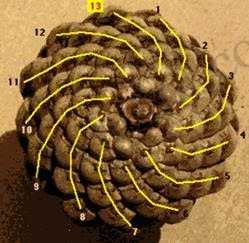
Quả thông này có 2 hệ đường xoắn ốc ngược chiều nhau, một hệ gồm 8 và hệ kia 13 đường. 8 và 13 là 2 số liên tiếp thuộc dãy Fibonacci

Một quả thông khác, không chỉ nhỏ hơn mà còn có các hệ đường xoắn ốc khác. Nó có 1 hệ 5 đường và 1 hệ 8 đường xoắn ốc. 5 và 8 là 2 số liên tiếp thuộc dãy Fibonacci.

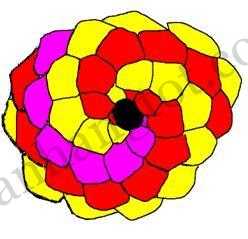
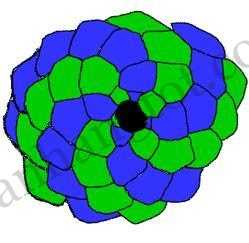
Quả thông nhỏ với 2 hệ đường xoắn ốc, gồm 5 và 8 đường

4. Ф và sự đâm chồi của cây

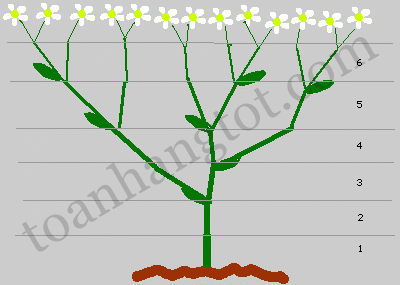
Nhiều loài cây biểu hiện dãy số Fibonacci trong số lượng các “điểm phát triển” (nút) mà nó có. Khi một cây mọc cành non, thì cành đó phải lớn lên một thời gian, trước khi đủ khỏe để bản thân nó có thể sinh cành non mới. Nếu mỗi tháng cây mọc cành mới tại các nút ấy, thì chúng ta có hình vẽ minh họa như trên. Số lượng các nút mỗi thời điểm luôn là một con số Fibonacci.

Một trong những loài cây phát triển rất giống với hình trên là loài cây Achillea ptarmica.

5. Ф và sự mọc lá của cây xanh

Nhiều loài cây cũng có cách mọc lá tuân theo các số Fibonacci. Nếu chúng ta quan sát kỹ sẽ thấy lá cây mọc trên cao thường xếp sao cho không che khuất lá mọc dưới. Điều đó có nghĩa là mỗi lá đều được hưởng ánh sáng và nước mưa, cũng như nước mưa sẽ được hứng và chảy xuống rễ đầy đủ nhất dọc theo lá, cành và thân cây.

Nếu từ một lá ngọn làm khởi đầu, xoay quanh thân cây từ trên xuống dưới, lá sang lá, đếm số vòng xoay đồng thời đếm số chiếc lá, cho đến khi gặp chiếc lá mọc đúng phía dưới lá khởi đầu, thì các số Fibonacci xuất hiện.

Nếu chúng ta đếm xoay theo hướng ngược lại, thì sẽ được một con số vòng xoay khác (ứng với cùng chừng ấy lá).

Kỳ lạ là: Con số vòng xoay theo 2 hướng, cùng với số lá cây mà chúng ta gặp khi xoay, tất cả sẽ tạo thành 3 con số Fibonacci liên tiếp nhau!

Ví dụ:Trong ảnh cây dưới, lấy lá (x) làm khởi điểm, ta có 3 vòng quay thuận chiều kim đồng hồ trước khi gặp lá (8) nằm đúng phía dưới lá (x), hoặc là 5 vòng nếu quay theo ngược chiều kim đồng hồ. Vượt qua tổng cộng 8 lá. 3,5,8 là 3 số liên tiếp trong dãy Fibonacci.

Các chiếc lá được đánh số khi quay vòng quanh thân từ trên xuống dưới, bắt đầu từ (x) rồi đến 1,2,3,… Kinh ngạc thay, mỗi chiếc lá liền kề cách nhau khoảng 222.5°, tức là chính xác 0,618 vòng tròn. 0,618 chính là 1/Ф

Chiếc lá (3) và (5) là những chiếc lá phía dưới gần lá khởi điểm (x) nhất, rồi xuống tiếp nữa là lá (8) rồi (13).

Lá số	Số vòng quay thuận chiều kim đồng hồ	Số vòng quay ngược chiều kim đồng hồ
3	1	2
5	2	3
8	3	5
13	5	8

Định luật này đúng cho cả các lá tiếp theo (21), (34)… Trên các cột và các hàng đều là những con số liên tiếp thuộc dãy Fibonacci!

Chỉ một cái cây bình thường nhưng ta thấy tỉ lệ vàng xuất hiện dày đặc như thế nào.

Có nhà nghiên cứu ước đoán rằng: 90% các loài cây có sự xếp lá tuân theo dãy số Fibonacci, theo cách này hay cách khác.

Gọi cách xếp lá của cây trong ví dụ trên là 3/8 (3 vòng đầu tiên, từ ngọn trở xuống đi qua 8 lá).

Điểm danh vài loài cây quen thuộc khác tuân theo dãy Fibonacci :

1/2	cây gỗ đu, cây gỗ đoan, cây chanh, cỏ
1/3	cây gỗ dẻ, cây phỉ, cây mâm xôi, nhiều loài cỏ
2/5	cây sồi, cây anh đào, cây táo, cây mận, cây cúc bạc
3/8	cây bạch dương, cây hoa hồng, cây lê, cây liễu
5/13	cây liễu đuôi sóc, cây hạnh nhân

Vạn vật muôn hình muôn vẻ trong vũ trụ dường như không tuân theo một trật tự phổ quát nào. Nhưng thực ra ẩn giấu đằng sau sự phong phú đa dạng đó, vẫn tồn tại một nguyên tắc chung cho tất cả.

6.Ф và Súp lơ

Đây là ảnh một cây xúp lơ thông thường. Nếu trông kỹ, ta có thể thấy một điểm giữa, ở đó những bông hoa là nhỏ nhất. Nhìn kỹ thêm, ta lại thấy những bông hoa tí xíu này được sắp xếp trên những đường xoắn ốc xung quanh điểm trung tâm kể trên, theo cả 2 hướng. Dễ dàng đếm được 5 đường xoắn ngược và 8 đường thuận chiều kim đồng hồ.

Xúp lơ kiểu Roman, bề ngoài và mùi vị vừa giống cải xanh vừa giống xúp lơ. Mỗi phần tử nhỏ nổi lên và giống với toàn thể nhưng có kích thước bé hơn, khiến các vòng xoắn nổi lên rất rõ ràng. Có 13 vòng xoắn ngược và 21 vòng xoắn thuận chiều kim đồng hồ.

7. Ф và các mầm cây dưới kính hiển vi điện tử

Mầm cây vân sam Na Uy này tuân theo quy luật dãy Fibonacci, gồm một hệ 8 đường và một hệ 13 đường xoắn ốc

Mầm cây Atisô này cũng có cách sắp xếp theo dãy Fibonacci, gồm các hệ 34 và 55 đường xoắn ốc

Luôn là Fibonacci và Ф ?

Vài loài hoa có 6 cánh hoa, và 6 không thuộc dãy Fibonacci. Trong hình là hoa huệ tây, hoa thủy tiên và hoa loa kèn đỏ. Nhưng nhìn kỹ thì chúng thực chất có 2 lớp cánh hoa trong – ngoài, mỗi lớp gồm 3 cánh hoa, và 3 là số Fibonacci.

Hoa huệ tây, hoa thủy tiên, hoa loa kèn đỏ có 6 cánh hoa, chia làm 2 lớp mỗi lớp 3 cánh. Như vậy các loài này thực chất vẫn tuân theo dãy Fibonacci

Thực tế cũng có rất ít loài cây có số lượng cánh hoa không phải là số Fibonacci, như loài hoa vân anh. Loài ớt ngọt đôi khi không có 3 mà lại có 4 múi.

Hoa vân anh có 4 lá, còn ớt ngọt đôi khi có 4 múi chứ không phải 3. Như vậy trong tự nhiên cũng có ít loài thực vật không tuân theo dãy Fibonacci

Sau đây là một vài ví dụ khác:

Một loài xương rồng có 4 và 7 vòng xoắn

Loài xương rồng này có 2 hệ gồm 11 và 18 vòng xoắn

Xương rồng Echinocactus Grusonii Inermis có 29 múi

Có một chuỗi số khác là dãy số Lucas, bắt đầu bởi số 2 và 1, rồi sau đó giống như dãy số Fibonacci chúng có quy luật là số sau bằng tổng 2 số liền trước.

Cuối cùng ta có dãy số Lucas như thế này: 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 …

Ta có: 3/1=3 4/3=1,333… 7/4=1,75 11/7=1,5714… 18/11=1,6363… 29/18=1,6111… 47/29=1,6206…

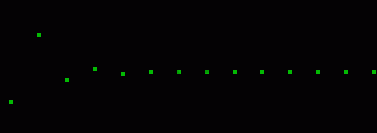
Đồ thị dãy số Lucas cũng tương tự như dãy Fibonacci. Điều đáng quan tâm là: Ln cũng tiến về Ф = 1,6180339… khi n tiến tới vô cùng

Bạn có thấy 4, 7, 11, 18, 29 đều xuất hiện trong các hình thực vật ở trên?

Như vậy các ngoại lệ không thuộc dãy Fibonacci thì lại thuộc một dãy số tương tự, điển hình là dãy Lucas. Rốt cuộc chạy trời không khỏi nắng, đại đa số thực vật đều liên quan đến con số Ф = 1,618 bí ẩn này không ít thì nhiều.

8. Ф và sự phân chia tế bào

Dưới đây trình bày một trong vài kiểu phân chia tế bào sinh vật trong thực tế.

Ban đầu chỉ có 1 tế bào, ta gọi đó là tế bào mẹ gốc A00.

Lần phân chia thứ 2: A00 sinh ra tế bào mẹ A01, sinh tế bào con A10, và một tế bào con A-1 (không sinh sản). Giờ có 3 tế bào tất cả là A01, A10, và A-1.

Lần phân chia thứ 3: A01 sinh ra A02, A10 sinh ra A11 và A20. A-1 vô sinh. Giờ có 4 tế bào A02, A10, A11, A20.

Lần phân chia thứ 4: Tế bào A02 không sinh sản mà trở thành A03. Giờ có 7 tế bào là A03, A11, A20, A12, A20, A21,A30.

Lần phân chia thứ 5: A03 chết. A12 không sinh sản trở thành A13. Giờ có 11 tế bào là A12, A20, A21, A30, A13, A21, A30, A22, A30, A31, A40.

Lần phân chia thứ 6: Giờ có 18 tế bào tất cả: A13, A21, A30, A22, A30, A31, A40, A22, A30, A31, A40, A23, A31, A40, A32, A40, A41, A50.

Lần phân chia thứ 7: Tất cả có 29 tế bào… vv…

Vậy số tế bào trong mỗi lần phân chia là 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843 … Đó chính là dãy Lucas, có liên hệ chặt chẽ với tỉ lệ vàng Ф…….

Các nhà minh triết Tây phương cổ xưa thường giỏi về nhiều lĩnh vực khoa học khác nhau. Có trí tuệ lại có đức, họ cảm nhận được sự vĩ đại của Tạo Hóa, hiểu rằng vũ trụ không phải tự nhiên sinh ra mà là được tạo dựng bởi uy lực vô cùng của Ngài.

Người Do Thái cổ quan niệm rằng Đấng tạo hóa (Elohim) tạo nên Trời Đất từ khoảng trống tối tăm hỗn độn.

Đáng kinh ngạc là ở mảnh đất Đông phương xa xôi với văn hóa khác biệt hoàn toàn, nhưng các minh triết cổ đại cũng đều đồng quan điểm như vậy. Người Đông phương cổ xưa cho rằng vũ trụ là một thể sinh mệnh.

Đức Lão Tử nói: “Có một vật sinh ra từ lúc hỗn nguyên, có từ trước khi Trời và Đất được sinh ra, yên lặng vô hình, độc lập mà không thay đổi, vận hành tuần hoàn mà không ngừng nghỉ, có thể là mẹ của vạn vật trong vũ trụ. Ta không biết tên là gì, bèn gọi là Đạo”.

Những người theo Phật giáo nguyên thủy cho rằng muôn vật sinh ra từ Hỗn nguyên (Sunyata) và Đấng chí tôn (Dharmakaya) là bất sinh bất tử vô hình.

Người thời nay hoàn toàn không biết người xưa tư duy như thế nào, quan sát vạn vật vũ trụ ra sao, phát triển đến trình độ cao siêu đến đâu. Không ai bảo đảm được là người thời nay thông minh và sáng suốt hơn họ, vì vậy chúng ta không thể nào phớt lờ những hiểu biết của họ, đặc biệt là về vũ trụ và nhân loại.

“Số Ф có mặt khắp nơi trong tự nhiên, rõ ràng điều đó vượt quá sự trùng hợp, và vì vậy người cổ xưa cho rằng con số Ф hẳn đã được tiền định bởi Đấng Sáng Thế. Các nhà hóa học buổi ban đầu đã tuyên bố 1,618 là Tỉ Lệ Thần Thánh”.

“… khía cạnh gây sửng sốt thực sự của Ф lại nằm ở vai trò của nó với tư cách là một nhân tố xây dựng mang tính nền tảng trong tự nhiên. Thực vật, động vật và thậm chí cả con người đều có những thuộc tính về kích thước gắn chặt với tỉ số giữa Phi và 1 tới một độ chính xác kỳ bí”.

“… các đường trôn ốc trên quả thông, cách sắp xếp lá trên những nhánh cây, các vạch trên bụng côn trùng…, tất cả đều tuân theo Tỉ Lệ Thần Thánh đến mức kinh ngạc”.

(Trích dẫn trong “Mật mã Da Vinci”)

Trang bìa cuốn sách lừng danh Mật mã Da Vinci

9. Ф và đàn Ong mật

Có trên 30.000 loài ong và phần lớn trong số chúng sống cuộc đời cô độc. Loài ong gần gũi với chúng ta nhất là ong mật. Chúng sống thành đàn trong một tổ ong, và chúng có một cây phả hệ rất khác thường. Cây phả hệ này tuân theo quy luật dãy số Fibonaci và tỉ lệ vàng.

Một trong những điều kỳ lạ nhất của ong mật là: không phải con ong nào cũng có cả cha và mẹ!

Trong đàn ong mật có một con cái đặc biệt gọi là ong chúa, chuyên đẻ trứng. Các ong cái khác không đẻ trứng mà chuyên môn làm việc gọi là ong thợ. Ong đực không làm việc.

Ong mật đực sinh ra từ trứng không thụ tinh của ong chúa, cho nên ong đực chỉ có mẹ mà không có cha.

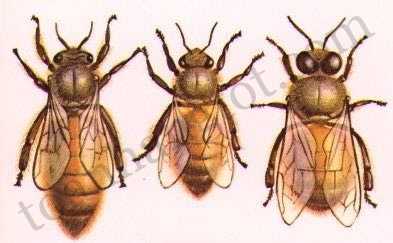
Ong chúa, ong thợ và ong đực có hình thái cơ thể khác nhau xa

Ong cái sinh ra khi ong chúa giao phối với một con ong mật đực và vì thế ong cái có cả cha lẫn mẹ. Thường thì ong cái lớn lên trở thành ong thợ, nhưng có một số ít được nuôi nấng bằng một dưỡng chất đặc biệt gọi là sữa ong chúa, khiến chúng phát triển trở thành ong chúa và sẵn sàng ra ngoài để tìm chỗ xây dựng một đàn ong mới.

Vậy ong cái có cả cha lẫn mẹ, trong khi ong đực chỉ có mẹ.

Xét cây phả hệ của một ong mật đực:

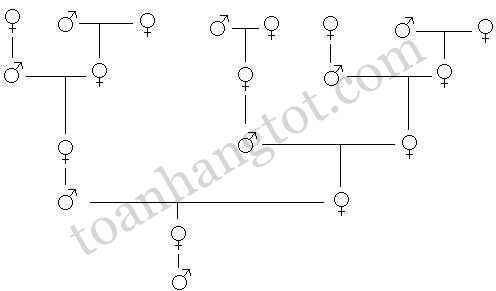
Có 1 mẹ
Có 2 ông bà
Có 3 ông bà cụ
Có 5 ông bà kị
vv…
Như vậy chúng ta lại có 2 dãy Fibonaci trong cây phả hệ này:

Số lượng	Cha mẹ	Ông bà	Cụ	Kị	(Trên kị)
Ong mật đực	1	2	3	5	8
Ong mật cái	2	3	5	8	13

(The Fibonacci Sequence as it appears in Nature của S.L.Basin trong Fibonacci Quarterly, tập 1, năm 1963, trang 53 – 57)

10. Ф và con bướm

Có rất nhiều loài côn trùng có kích thước cơ thể trùng khớp với các con số thuộc dãy Fibonacci, liên quan chặt chẽ với Tỉ lệ Vàng. Hoạt hình dưới là phân tích các kích thước của một con bướm.

Cây thước đặc biệt trên hình có khoảng cách giữa các đầu nhọn tuân theo dãy Fibonacci

11. Ф và cơ thể người

Bức vẽ nổi tiếng “Vitruvian Man” của danh họa Leonardo da Vinci

Nếu trong thực tế cơ thể bạn đúng theo các tỉ lệ sau đây thì chắc chắn trông rất cân đối và đẹp:
– Chiều cao / đỉnh đầu đến đầu ngón tay = Ф
– Đỉnh đầu tới đầu ngón tay / đỉnh đầu tới rốn (hoặc cùi chỏ) = Ф
– Đỉnh đầu tới rốn (hoặc cùi chỏ) / đỉnh đầu tới ngực = Ф
– Đỉnh đầu tới rốn (hoặc cùi chỏ) / chiều rộng đôi vai = Ф
– Đỉnh đầu tới rốn (hoặc cùi chỏ) / chiều dài cẳng tay = Ф
– Đỉnh đầu tới rốn (hoặc cùi chỏ) / chiều dài xương ống quyển = Ф
– Đỉnh đầu tới ngực / đỉnh đầu tới gốc sọ = Ф
– Đỉnh đầu tới ngực / chiều rộng của bụng = Ф
– Chiều dài của cẳng tay / chiều dài bàn tay = Ф
– Vai đến các đầu ngón tay / khuỷu tay đến các đầu ngón tay = Ф
– Hông đến mặt đất / đầu gối đến mặt đất = Ф
– Gọi độ dài từ rốn lên đến đỉnh đầu là x, độ dài từ rốn xuống đến chân là y. Độ dài 1 dang tay gọi là a. Nếu x/y = a/(x+y) = 1,618 = Ф, thì đó là thân hình của các siêu người mẫu. Điều này hoàn toàn là sự thật vì các hãng thời trang lớn đều tuân thủ nghiêm ngặt quy định này khi tuyển người mẫu.

12. Ф và bàn tay người

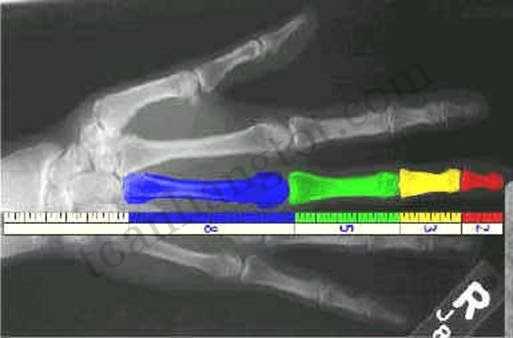
Thường thì 4 đốt xương của các ngón tay tuân theo dãy số Fibonacci: 2, 3, 5, 8

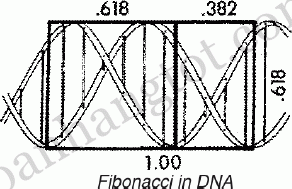
13. Ф và ADN

Phân tử ADN cũng liên quan đến Ф. Mỗi chu kỳ xoắn kép của nó dài 34 Angstrom rộng 21 Angstrom. Và 21 và 34 là 2 số liên tiếp thuộc dãy Fibonacci.

14. Ф và Sao Thổ

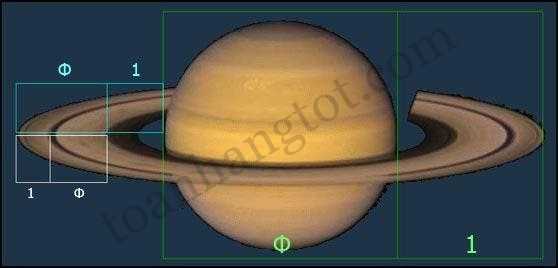
Sao Thổ nổi tiếng với vành đai tuyệt đẹp của nó. Ít ai ngờ rằng các kích thước của nó như đường kính, khoảng cách vành đai, vv… có nhiều liên quan đến tỉ lệ vàng Ф.

15. Ф, Trái Đất và Mặt Trăng

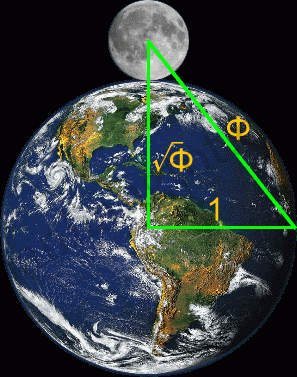
Bán kính Trái Đất	6.378,10
Bán kính Mặt Trăng	1.735,97
Tổng cộng = cạnh góc vuông lớn của tam giác trên hình	8.114,07
Cạnh huyền	10.320,77
Tỉ số Cạnh huyền/cạnh góc vuông nhỏ	Ф = 1,618
Nếu quy ước bán kính trái Đất là 1 thì ta có số đo như hình vẽ trên

16. Ф và các thiên hà

Hình chữ nhật vàng là hình chữ nhật có tỉ số chiều dài : chiều rộng = Ф. Đường xoắn ốc Fibonacci, nằm bên trong hình chữ nhật vàng.

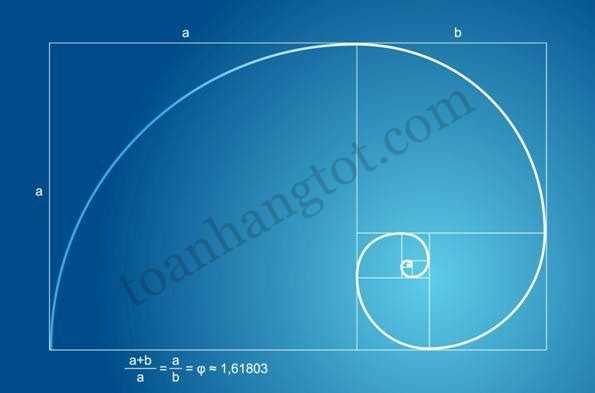
Trong vũ trụ có rất nhiều thiên hà xoắn ốc đúng theo đường xoắn ốc Fibonacci. Ví dụ dải thiên hà NGC 5194 cách dải ngân hà của chúng ta 31 triệu năm ánh sáng.

17. Ф trong thế giới lượng tử

“Tỷ lệ vàng”, xấp xỉ với 1,618, có thể được tìm thấy trong nhiều khía cạnh của đời sống chúng ta, bao gồm sinh học, kiến trúc và nghệ thuật.

Nhưng chỉ mới đây, người ta mới phát hiện ra rằng tỷ lệ đặc biệt này cũng được phản ánh trong cấp độ na-nô, nhờ các nhà nghiên cứu thuộc Đại học Oxford của Anh Quốc, Đại học Bristol, Phòng thí nghiệm Rutherford Appleton, và Viện Vật liệu và Năng lượng Helmholtz-Zentrum Berlin của Đức (HZB).

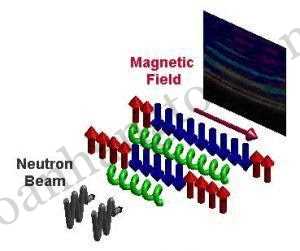
Nghiên cứu của họ, được công bố trong tạp chí Khoa học ngày 8 tháng 1, đã xem xét các chuỗi nguyên tử cobalt niobate mang từ tính liên kết với nhau với độ rộng chỉ có một nguyên tử để khảo sát Nguyên lý bất định của Heisenberg. Họ đặt một từ trường tại góc phải của một mô-men nội tại (spin) thẳng hàng của các chuỗi từ tính để có thêm sự bất định lượng tử. Tùy theo các biến đối của hướng từ trường, những nam châm nhỏ này bắt đầu cộng hưởng từ.

Các hạt neutron được bắn vào các nguyên tử cobalt niobate để phát hiện các nút cộng hưởng. “Chúng tôi đã tìm thấy một chuỗi (tỷ lệ) các nút cộng hưởng: Hai nút đầu tiên cho thấy một mối quan hệ hoàn hảo với nhau. Các tần số của chúng (pitch) nằm theo tỷ lệ 1,618… là tỷ lệ vàng nổi tiếng trong nghệ thuật và kiến trúc”, nhà nghiên cứu trưởng, Tiến sĩ Radu Coldea tại Đại học Oxford nói trong một thông cáo báo chí. “Nó phản ánh một đặc tính tuyệt đẹp của hệ thống lượng tử – tính đối xứng ẩn.”

Tiến sĩ Alan Tennant, người dẫn đầu nhóm nghiên cứu tại Berlin nói: “Những khám phá như thế này đang dẫn các nhà vật lý tới sự suy luận rằng thế giới lượng tử, cấp nguyên tử có thể có trật tự cơ bản của riêng nó. Những điều ngạc nhiên tương tự có thể đang chờ đợi các nhà nghiên cứu ở các vật liệu khác trong trạng thái lượng tử tới hạn.”

“Hai phát hiện vĩ đại nhất của hình học, một là định lý Pythagore, và hai là tỷ lệ vàng – một thứ có thể so sánh là quý như vàng, còn thứ kia có giá trị như một viên ngọc quý”

Kepler

18. Ф và Bí mật của vẻ đẹp hài hòa 

Tỷ lệ vàng khi được áp dụng trong nghệ thuật đều mang đến cho con người 1 cảm giác đẹp hài hòa và dễ chịu một cách khó giải thích. Do đó, nó được giảng trong các môn học như nghệ thuật, kiến trúc, mỹ thuật, trang trí, hội họa, điêu khắc, nhiếp ảnh, vv… như là một quy luật, tương hợp kỳ lạ với óc thẩm mỹ tự nhiên của con người.

Apple vận dụng tỷ lệ vàng trong các thiết kế của mình, ngay cả trang Twitter cũng vận dụng nó, các mẫu logo của các công ty hàng đầu thế giới cũng áp dụng tỉ lệ vàng. Tờ báo mà bạn đang đọc, màn hình vi tính, thẻ tín dụng, toà nhà cao ốc, cánh hoa, lá cây – tất cả mọi thứ đều được tạo lập dựa trên một nguyên tắc, một tỷ lệ, một giá trị cân đối. Dường như Tạo hóa đang tiết lộ với chúng ta về bí mật của bản thiết kế mà Ngài đưa vào trong mỗi phần tử của vũ trụ.

Qua nhiều thế kỷ, cái đẹp tuyệt đối của nghệ thuật và óc thẩm mỹ của loài người chưa bao giờ chệch quá xa khỏi tỷ lệ kỳ bí này.

Vẻ đẹp của cơ thể con người cũng có liên quan tới số Ф. Thương của phép chia chiều cao từ đầu tới chân với khoảng cách từ rốn tới chân ≈ 1.618, thể hiện sự hài hoà cân đối của cơ thể. Chúng ta cũng có thể tìm ra kết quả tương tự trong tỷ lệ của chiều dài cái đầu với khoảng cách từ mắt tới cằm; hay tỷ lệ của khoảng cách từ mũi tới cằm trên khoảng cách từ môi tới cằm. Những tỷ lệ của gương mặt càng tiến gần tới tỷ lệ này thì gương mặt càng hài hoà cân đối. Thậm chí sở thích của chúng ta dường như cũng đã được định sẵn.

Trong một cuộc nghiên cứu nổi tiếng do Gustav Fechner tiến hành năm 1876, trong đó người ta được yêu cầu chọn một hình chữ nhật ưng ý nhất trong số một bộ các hình chữ nhật có kích thước từ một vuông đến gấp đôi. Kết quả là kích thước hình chữ nhật càng gần với hình chữ nhật vàng thì số người lựa chọn càng tăng lên. Ông còn nghiên cứu xa thêm bằng cách đo đạc tỉ lệ của các cửa sổ và cửa ra vào của các ngôi nhà, và phát hiện phần lớn chúng xấp xỉ tỉ lệ vàng. Điều đó cho thấy óc thẩm mỹ đã đưa nhân loại đến gần tỉ lệ vàng mà bản thân họ cũng không biết.

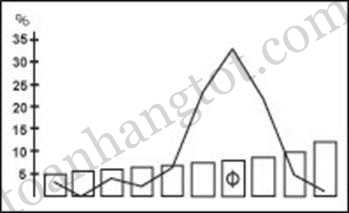
Tỉ lệ các cạnh của hình chữ nhật càng gần Ф thì càng bắt mắt.
Hình chữ nhật có chiều dài / chiều rộng = Ф được gọi là hình chữ nhật vàng

Cả loài người vẫn không thể giải thích được tại sao vô số những thực thể hữu cơ lẫn vô cơ tìm thấy trong tự nhiên lặp đi lặp lại tỷ lệ đặc biệt trên. Nguyên nhân đằng sau con số chi phối sự cân đối hài hoà và vẻ đẹp của toàn thể vũ trụ và nhân loại ấy là gì? Câu hỏi này đã thu hút sự quan tâm đặc biệt của rất nhiều người trong hàng thiên niên kỷ qua, nhưng cho đến ngày nay nó vẫn tiếp tục là một điều bí ẩn.

19. Ф và các công trình kiến trúc

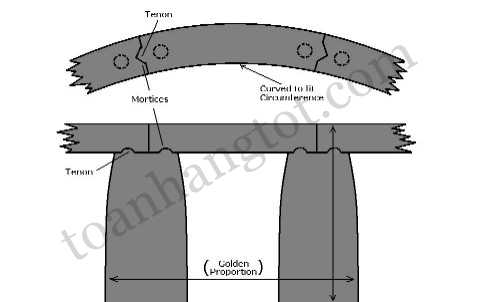
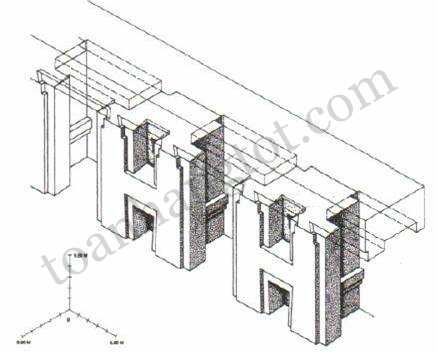
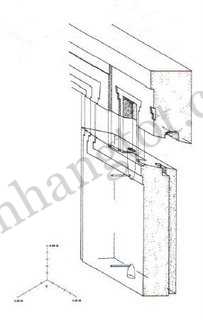
Tỉ lệ vàng đã được áp dụng trong các kích thước kiến trúc của các công trình nổi tiếng như đền Parthenon Hi Lạp, các kim tự tháp Giza và thậm chí của cả tòa nhà trụ sở Liên hợp quốc tại New York. Một số kiến trúc Việt Nam cũng thể hiện tỉ lệ này.

“Thước tầm” thời xưa của Việt Nam với những số đo xuất phát từ các kích thước của con người cũng tuân thủ quy luật của Tỷ Lệ Vàng. Tỉ lệ giữa “khoảng nằm” và “khoảng đứng” luôn là một số ≈ Ф, mặc dù con số ấy có sai khác đôi chút giữa các phường thợ khác nhau.

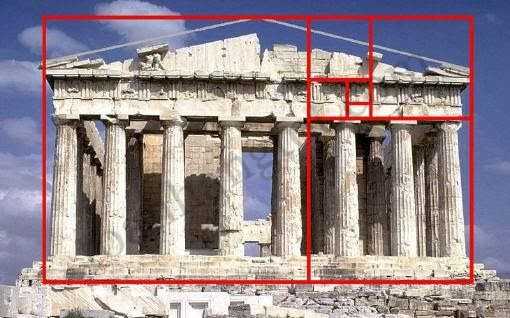
“Hình chữ nhật vàng” trong thiết kế đền thờ Parthenon tại Hy Lạp

Tháp CN tại Toronto, Canada là tòa tháp cao nhất thế giới, cũng được thiết kế theo tỉ lệ vàng. Tỉ số giữa tổng chiều cao tháp so với độ cao của đài quan sát là 553,33m : 342m = 1,618 = Ф

Kiến trúc tuyệt mỹ của thế giới – Taj Mahal – xây năm 1648, cũng chứa trong nó tỉ lệ vàng

Tháp Rùa, Hà Nội

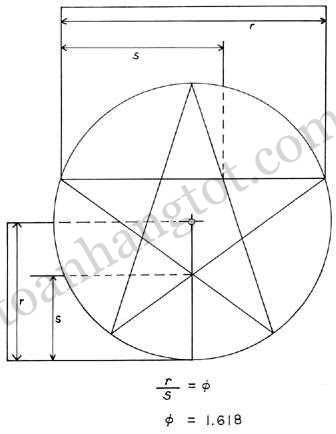
* Một công cụ hay được dùng trong nghiên cứu và ứng dụng Tỉ lệ vàng là chiếc compa Tỉ lệ vàng.

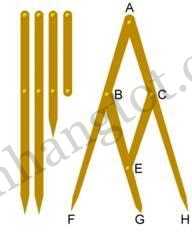
Compa tỉ lệ vàng. Ta có ABEC là hình bình hành, nên FG/GH=FB/BA= Ф

Một số kiến trúc khác có thiết kế phù hợp với tỉ lệ vàng:

20. Ф và Quy tắc phần ba trong nhiếp ảnh

Hằng số Ф chi phối hầu như mọi thiết kế của tự nhiên nói chung và các sinh thể nói riêng, tạo ra vẻ đẹp hài hòa. Tỉ lệ vàng là một khuôn mẫu đã đi vào sách vở và vẫn được giảng dạy cho đến ngày nay, do đó việc người ta áp dụng nó trong nhiếp ảnh là một điều dễ hiểu.

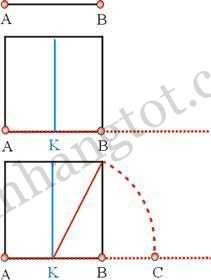
Cách dựng “hình chữ nhật vàng”

Trong nhiếp ảnh, người ta thường nói đến quy tắc phần ba: 1+0,618+1.

Các nhiếp ảnh gia giàu kinh nghiệm đều biết Tỉ lệ vàng trong việc sắp xếp bố cục, và sử dụng chúng nhuần nhuyễn một cách gần như tự động, không phải suy nghĩ. Nhưng trước khi đạt được đến trình độ ấy thì họ thường phải học hỏi và luyện tập nhiều. Dưới đây là một số bức ảnh chụp có sử dụng quy tắc này.

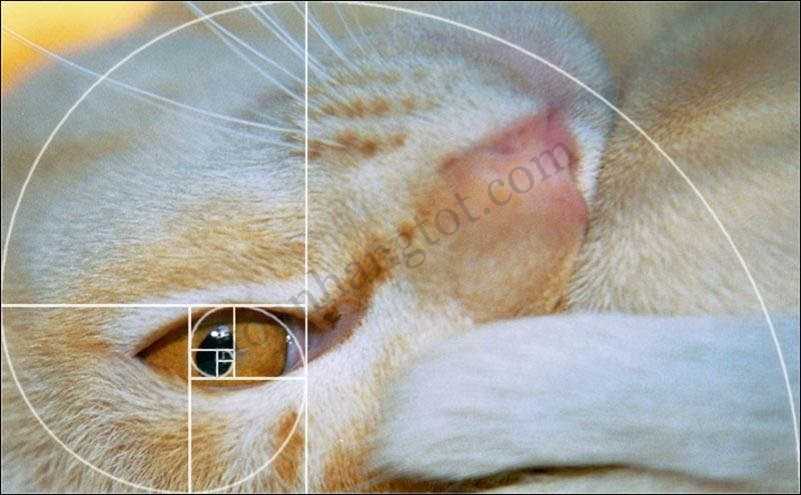
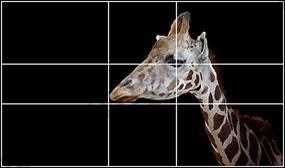
Khi càng đặt nhiều đường “Phi” trùng với các đường nét chính của chủ thể, thì tính hấp dẫn càng cao hơn

Như với thí dụ trên, con mắt của con ngựa được đặt ngay một “giao điểm” của “Phi”.
Một ví dụ khác, với hình trên, cách bố trí điểm “Phi” được đặt ở ngay mắt trái của chủ thể, để tạo chủ điểm hấp dẫn.

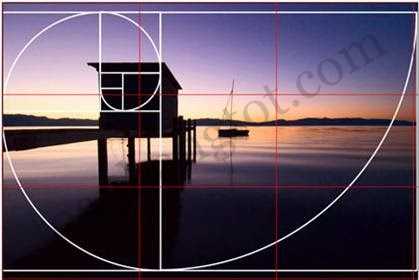
Đường chân trời được đặt ngay tại đường “Phi” trên, ngôi nhà thờ, và con đường tạo mối liên kết với nhau

Để luyện tập cách sử dụng tỉ lệ vàng trong nhiếp ảnh, độc giả có thể truy cập và xem tại đây : http://photoinf.com

21. Lịch sử bí ẩn của Tỉ lệ Thần thánh

Franziskanermönch Luca Pacioli di Borgo San Sepolcro (1445 – 1514) – một giáo viên toán ở Perugia, đã gọi tỉ lệ này là Tỉ lệ Thần thánh (“De Divia Proportione”) và cho ra đời 3 cuốn sách vào năm 1509. Trong cuốn đầu tiên ông chỉ nêu các vấn đề toán học. Trong cuốn thứ hai ông nêu ra sự liên quan giữa bản viết của một người La Mã là Vitruvius từ thế kỉ 1 trước công nguyên với Kiến trúc, trong đó còn nói về việc lấy tỉ lệ người như là một khuôn mẫu.

Adolf Zeising (1854) đưa ra mối liên quan giữa tỉ lệ vàng và Nghệ thuật. Ông tin chắc rằng mọi vật thể sống đều tuân theo một qui luật tự nhiên về thẩm mỹ, mà cơ bản ở đây là tuân theo Tỉ lệ vàng. Ông đã tìm kiếm và nhận thấy rằng tỉ lệ vàng có ở khắp mọi nơi. Nghiên cứu của ông đã gây tiếng vang lớn trong dư luận.

Martin Ohm (em trai của George Simon Ohm với định luật Ohm nổi tiếng) từng đưa Tỉ lệ Vàng vào giảng dạy trong một giáo trình toán. Cụm từ sectio aurea (tỉ lệ Thần thánh) cũng được đưa ra trong thời kì này.

Vào những năm đầu thế kỉ 20 xuất hiện một bài viết về quan sát tỉ lệ vàng của một người Rumani tên là Matila Costiescu Ghyka. Ông đã kết hợp giữa lý thuyết của Pacioli và nghiên cứu về thẩm mỹ của Zeising và kết luận Tỉ lệ vàng như là một bí ẩn của vũ trụ, xuất hiện khắp mọi nơi.

Trước đây người ta vẫn cho rằng một người La Mã là Vitruvius sống cách đây gần 2.100 năm đã phát minh ra tỉ lệ vàng. Tuy nhiên Tỉ lệ Vàng đã được tìm thấy trong các kiến trúc cổ xưa hơn nhiều, ví dụ Kim tự tháp Lớn của Ai Cập.

Cho đến ngày nay nhân loại vẫn không biết kiến thức về Tỷ lệ Vàng có từ bao giờ.

Vào mùng 4 Tết vừa qua, tức ngày 23/2, cư dân mạng hết sức sôi sục về tin một chú heo quỳ gối dập đầu trước cửa chùa. Theo thông tin mới nhất nhận được, chú heo đã bị đưa đến lò mổ đúng ngày hôm đó, ông chủ của chú heo vô cùng hối hận về việc này vì ông biết chuyện của chú heo quá muộn.

>> Chú heo quỳ gối dập đầu trước cửa chùa chỉ rời đi sau khi nghe kinh Phật

Cư dân mạng lại tiếp tục sôi sục, họ cho rằng heo cũng là loài động vật có linh tính, nói đúng hơn là vạn vật đều có linh, theo đó câu chuyện về chuyển sinh lại trở thành chủ đề nóng được bàn tán sôi nổi.

Tờ Đô Thị Ôn Châu” của Trung Quốc đưa tin, con heo này đã quỳ rất lâu trước một ngôi chùa gần cầu Vĩnh Gia, thôn Thản Đầu, thành phố Ôn Châu. Chú heo là vật sở hữu của một người dân trong thôn. Theo lời người chủ kể, hôm mùng 4 Tết, con heo này và 2 con khác, vì chê thức ăn lợn ít quá, đã rủ nhau chạy trốn khỏi chuồng lợn, người chủ đến tận buổi chiều mới tìm thấy, và tối hôm đó đưa heo đi giết luôn.

Ông Hoàng, người chủ của con heo, nói rằng, sau khi con heo bị giết, ông mới biết chuyện, lúc xem video, ông rất đỗi ngạc nhiên. Theo kinh nghiệm nuôi heo của ông Hoàng, một con heo khi gặp chuyện làm chúng sợ, sẽ lập tức chạy ngay, chứ không thể thực hiện tư thế này. Việc giết chú heo làm ông Hoàng rất ân hận.

Hôm mùng 4 Tết, con heo này đầu hướng vào cửa chùa, 2 chân trước quỵ xuống, 2 tai hướng phía trước, đầu mũi như cuối xuống, người ta đuổi thế nào nó cũng không đi, và chỉ rời đi sau khi được nghe kinh Phật. Video ghi hình chú heo đã nhận được hơn 7 triệu 7 trăm lượt xem, và trở thành để tài làm nóng các diễn đàn.

Có người đùa rằng, “đây là Trư Bát Giới chuyển sinh, hy vọng được quy y Phật gia”. Cũng có người khác trên Weibo nói rằng, “Chúc mừng con heo này! Bị giết thì mới có thể đi đầu thai chuyển thế! Biết đâu lại được làm người! Người chủ không cần phải tự trách mình quá, đều là may mắn”. Đề tài chuyển thế luần hồi một lần nữa được thảo luận sôi nổi.

Trang Đai Kỷ Nguyên từng đưa tin về việc ông Mario Ramberg Capecchi, chuyên gia về luân hồi, thông qua các kết quả nghiên cứu, đã khẳng định luân hồi thực sự tồn tại.

Giáo sư Mario Ramberg Capecchi khẳng định luân hồi là có thật

Một số trường hợp trong nghiên cứu cho thấy, có người vì kiếp trước là động vật, nên kiếp này vẫn còn chút tác động lên tính cách và lối ứng xử; rồi cũng có người với kiếp trước là người, kiếp này lại chuyển sinh thành động vật.

Năm 1934, một câu chuyện có thật về luân hồi vẫn được lưu truyền cho đến ngày hôm nay. Đó là chuyện 1 con heo có tay người, sống ở trong sân vườn của chùa Bảo Hòa Thượng Hải. Một người là Định Tử Bình tiên sinh đã nhờ người chụp hình và đăng bài “Bằng chứng luân hồi của súc vật” để khuyến thiện. Hình ảnh và câu chuyện từng gây chấn động, và trở thành bằng chứng vững chắc chứng minh luân hồi là có thật, qua đó cho thấy thiện ác hữu báo.

Theo ghi chép của bài báo này, con heo thực ra chính là chuyển sinh của ác bá Thi Khánh Chung. Năm 1923, người này bị ốm nặng, tính mạng như chỉ mành treo trước gió. Khi đó, một vị hòa thượng vân du ngang qua, nói với y rằng: “Thí chủ đã tạo ác nghiệp quá nhiều, sau khi chết đi, thân sẽ bị đọa vào cửa súc sinh, và trở thành heo, nếu mau biết sám hối, thì tội có thể được giảm nhẹ”. Thi Khánh Chung biết mình còn không nhiều thời gian nữa, trong lòng rất hoảng sợ, hối hận vô cùng trước những tội ác và chuyện điên rồ đã gây ra trong đời này, ông liền giơ tay trái làm bán hợp chưởng, hành lễ với vị sư. Vị hòa thượng thở dài và nói: “Chỉ có tay này, hướng Phật thành tín, vậy bàn tay này có thể được miễn biến thành heo, dù sao cũng là thoát khỏi việc bị giết mổ”.

Sau khi ông Thi chết, làng bên có 1 con heo mẹ sinh ra một con heo có tay người. Khi con heo con này bước đi, cánh tay người không bao giờ chạm đất, thỉnh thoảng còn hợp chưởng, hành lễ với người. Người nhà ông Thi sau này biết chuyện, họ liền cho mua lại con heo và đưa vào đền Bảo Hòa phóng sinh nuôi dưỡng.

Cũng nói thêm về chuyện vạn vật có linh, âu cũng là chứng minh cho sự tồn tại của hiện tượng luân hồi, bởi động vật nếu là người chuyển sinh ắt chúng cũng có linh tính. Chú heo này có thể đã biết trước cái chết của mình, nên đã tìm đến cửa Phật bái lạy, hòng tỏ ý ăn năn chuộc tội cho lỗi lầm đã phạm nên mới đầu thai thành heo, nay mong được trở lại kiếp người.

Nhân đây, tôi cũng xin kể lại một câu chuyện thú vị tự mình vừa trải qua. Sáng nay, khi vừa thức dậy, tôi đã nghe tiếng động cơ chạy ra sau nhà, nhìn ra mới biết có người đang khởi động cưa máy để đốn hạ 2 cái cây. Chuyện không có gì đáng nói nếu cậu em tôi không buộc miệng rằng: “Tối qua tự dưng có mấy con chim kêu thét ầm ĩ bên cửa sổ, ai ngờ sáng nay lại có người cưa mất cái cây ngay trước cửa sổ này. Có lẽ tối qua, chúng đã biết sẽ bị mất chỗ ở”.

Bấy nhiêu cũng đủ để thấy rằng động vật là có linh tính, thậm chí có phần hơn con người khi biết trước cả tương lai. Thêm nữa, thuyết về luân hồi cũng là để răn dạy con người biết hành thiện để không tạo nghiệp vì làm chuyện trái lẽ trời.

Qua nhiều năm nghiên cứu, các nhà khoa học đã ghi nhận được hàng ngàn trường hợp đầu thai. Sau đây là một trường hợp luân hồi đáng lưu ý ở phương Tây.

>> Luân hồi tái sinh đầu thai chuyển kiếp (kỳ 1)
>> Luân hồi tái sinh đầu thai chuyển kiếp (kỳ 2)
>> Luân hồi tái sinh đầu thai chuyển kiếp (kỳ 3)

Trường hợp của bé James Leininger (sinh ngày 10/4/1998)

Cha của James là Bruce C. Leininger, một thạc sỹ chuyên ngành khoa học xã hội. Mẹ Andrea của cậu là một phụ nữ đa tài, giỏi về hội họa, múa, và văn học. Cô từng theo học ba lê tại New York và San Francisco. Sau khi tốt nghiệp trường trung học cô là một vũ công ba lê chuyên nghiệp suốt 10 năm trước khi quyết định nghỉ ngơi để chăm sóc gia đình.

Cậu bé James từ khi còn rất nhỏ đã không chơi với thứ gì khác ngoại trừ máy bay, cha mẹ cậu kể lại. Nhưng khi cậu bé lên 2 tuổi, những chiếc máy bay mà cậu yêu thích lại thường xuất hiện trong những cơn ác mộng lặp đi lặp lại tới 4 lần một tuần, làm James la hét và quẫy đạp dữ dội. Dường như bé đang chiến đấu với một cái gì đó hoặc là đang bị nhốt trong lồng, và cố gắng thoát ra ngoài. Cách duy nhất để bé thoát khỏi ác mộng là cha mẹ phải lay bé dậy. Trong giấc mơ, cậu bé thường la lớn: “Máy bay rơi bốc cháy, người đàn ông trẻ không thoát ra được”.

Andrea kể mẹ cô là người đầu tiên nghĩ rằng có thể James đang nhớ lại kiếp trước của mình.

Ban đầu, Andrea nói, cô rất hoài nghi. Cha mẹ James cho biết cậu bé chỉ xem các chương trình truyền hình thiếu nhi mà thôi, còn họ thì không hề xem các phim tài liệu thời Thế chiến thứ II hay bàn luận gì về chiến tranh cả. Trong một cuốn băng video thu vào năm James 3 tuổi, người ta thấy cậu bé xem xét kỹ lưỡng một chiếc máy bay như thể viên phi công đang kiểm tra trước khi bay vậy.

Một lần khác, Andrea mua cho cậu bé một chiếc máy bay đồ chơi và chỉ cho cậu xem một thứ trông như một trái bom bên dưới. James đã chỉnh cô ngay, bảo rằng đó là một drop tank (thùng chứa xăng phụ phía dưới thân máy bay, có thể thả rơi xuống nếu cần thiết). “Tôi chưa từng nghe nói về drop tank. Tôi còn không biết đó là cái gì nữa”.

Rồi những cơn ác mộng của cậu bé ngày càng tệ hơn. Mẹ của Andrea bảo cô nên đến gặp tiến sỹ Carol Bowman, một bác sỹ chuyên khoa trong lĩnh vực nghiên cứu luân hồi tái sinh. Bowman còn là tác giả của cuốn sách “Tiền kiếp của những đứa trẻ: Ký ức tiền kiếp ảnh hưởng đến con bạn như thế nào”, viết sau khi chính con trai của bà gặp phải những cơn ác mộng và những hồi tưởng lạ lùng tương tự như thế.

Andrea đã gọi điện cho bà tiến sỹ ngay lập tức. Với sự hướng dẫn của Bowman, Andrea bắt đầu khuyến khích James chia sẻ những kí ức của bé ngay sau cơn ác mộng. Kết quả là, những cơn ác mộng đã giảm hẳn. James cũng diễn đạt rõ ràng hơn về quá khứ của mình, Andrea kể lại.

Tiến sỹ Bowman cho biết James đang ở một lứa tuổi có thể dễ nhớ lại về kiếp trước nhất. Bà nói: “Chúng chưa gặp những tác động văn hóa, chưa bị những kinh nghiệm sống của kiếp này lấn át, nên ký ức có thể trào dâng dễ dàng hơn... Việc trẻ nhỏ mơ về tiền kiếp không phải là chuyện hiếm gặp. Chúng ta thường chú ý tới ác mộng bởi vì chúng quấy phá giấc ngủ, và thường là những câu chuyện xúc động và rất thực, giống như trường hợp của James vậy. Ác mộng thường tái diễn luôn, khi đứa trẻ hồi tưởng lại những sự kiện đầy kịch tính ấy mãi. Ở một mức độ nào đó, chúng đang tìm cách giải quyết cho những ký ức nhiễu loạn ấy. Khi Andrea đã biết được sự việc mà James nhớ lại trong giấc mơ – là chiếc máy bay rơi – điều đó đã giúp cậu bé vượt qua được chấn thương tinh thần”.

Nhưng tác dụng phụ của điều đó – đúng như tiến sỹ Bowman đã dự đoán trước – những hồi ức của James về chiếc máy bay rơi và về người đàn ông mà đã không thể thoát ra trở nên chi tiết hơn, thực tại hơn. James bắt đầu hồi tưởng lại trong khi tỉnh, một cách rõ ràng, về việc máy bay của cậu cất cánh khỏi mặt nước và quân Nhật đã bắn rơi nó như thế nào. James kể với cha là cậu từng lái một chiếc máy bay hiệu Corsair. Cậu bé còn nói cậu đã phục vụ trên chiếc hàng không mẫu hạm có tên là USS Natoma Bay trong cuộc chiến với Nhật Bản. Những chi tiết rõ ràng và kỳ lạ này đã buộc Bruce tiến hành một cuộc điều tra nghiên cứu với sự giúp đỡ của vợ để chứng minh tất cả chuyện này không phải là sự thật. Cả 2 vợ chồng hoài nghi và không muốn tin vào điều đó.

Tuy nhiên cuộc nghiên cứu kéo dài suốt gần 5 năm trời với hàng ngàn tài liệu, những cuộc phỏng vấn cá nhân và các nguồn tin của quân đội, Bruce và Andrea cuối cùng đã phải chắc chắn một điều: con trai họ có mối liên hệ kỳ lạ với một phi công Hải quân Hoa Kỳ trong cuộc chiến tranh thế giới thứ II, có tên là James M. Huston con, đã hy sinh vào năm 1945 trong khi đang làm nhiệm vụ, trên vùng trời Iwo Jima, Nhật Bản.

Những điều lạ lùng khi mới 20 tháng tuổi

Bruce và Andera kể rằng họ bắt đầu thấy những dấu hiệu lạ thường ngay từ khi James hơn 1 tuổi rưỡi. Andrea kể cậu bé cứ luôn luôn quấn quít bên những chiếc máy bay: Cậu chơi với máy bay đồ chơi suốt nhiều tiếng đồng hồ không biết chán và reo lên mỗi khi trông thấy một chiếc máy bay nào đó băng qua bầu trời.

Khi chuyển nhà từ Richardson, Texas, tới Lafayette vào tháng 2 năm 2000, Bruce đã dẫn James tới Bảo tàng Máy bay Cavanaugh tại Addison, Texas. Cậu con trai ông như bị thôi miên bởi những chiếc máy bay tại Viện bảo tàng ấy. Chú bé cứ thơ thẩn quanh quẩn lại khu vực Thế chiến II của Bảo tàng. Khi ông cố gắng đưa James trở về nhà sau gần 3 tiếng ở đó, James gào khóc. Để thỏa mãn sự tò mò và vỗ về cậu, Bruce đã mua cho cậu một băng video trình diễn máy bay Thiên thần Xanh Hải quân (Navy Blue Angels) tại Bảo tàng. James đã xem nó nhiều đến nỗi cuộn băng gần như nát cả ra.

Vào tháng 4 năm 2000, sau khi đã ổn định nơi ở mới tại Lafayette, những cơn ác mộng của James bắt đầu xuất hiện. Bruce và Andrea cho rằng ác mộng là do James chưa quen với ngôi nhà mới. Nhưng khi ác mộng diễn ra triền miên, thì cha mẹ cậu bé đã phải quan tâm đặc biệt đến con mình.

Trong lúc đó, thì những đồ dùng trong nhà đã phải hứng chịu bộ sưu tập máy bay của James. Cậu bé thả những chiếc máy bay đồ chơi của mình rơi đâm thẳng xuống mặt bàn và ghế. Andrea nhớ lại, vừa đưa tay chỉ vô số những vết trầy xước trên mặt bàn phòng khách. Chiếc bàn đã là bãi đáp cho máy bay của cậu bé. Máy bay đâm xuống mặt đất đã là một nỗi ám ảnh dai dẳng đối với James, đến nỗi khi bất kỳ ai đề cập đến bay lượn, thì James lập tức buột miệng kêu “Máy bay rơi cháy rồi”. Điều đó khiến Andrea rất lo lắng.

Từ tháng 7 cho tới tháng 9 năm 2000, James đã bắt đầu kể với cha mẹ rằng chiếc máy bay trong những ác mộng ấy đã bị quân Nhật bắn rơi sau khi cất cánh từ một con tàu trên mặt biển. Khi James được hỏi liệu cậu có biết viên phi công ấy là ai không, cậu chỉ đáp gọn “James”.

Andrea hỏi James loại máy bay mà cậu đã lái trong những giấc mơ, và cậu nói nó là một chiếc “Corsair”. Vậy là, sau nhiều lần cố lấy thêm thông tin sau những ác mộng ấy, Bruce và Andrea đã nghe James nói “Natoma“. Bất chợt nảy ý thử tìm hiểu thực hư, Bruce đã tìm kiếm trên mạng với từ khóa “Natoma”. Kết quả là: có tồn tại một tàu sân bay mang tên USS Natoma Bay, đóng tại Thái Bình Dương trong Thế chiến II. Bruce đã nghĩ rằng đó chỉ là một trùng hợp ngẫu nhiên thôi.

Vào tháng 10 năm 2000, lại thêm một mảnh câu đố đã được làm sáng tỏ. Sau một cơn ác mộng khác, James đã nói với cha mẹ cái tên Jack Larsen, và cậu bảo đó là Larsen mà cùng bay với James. Tháng sau, James lại có thêm một chút thông tin nữa làm kinh hoàng người cha vốn luôn nghi ngờ. Bruce lướt xem một quyển sách tựa đề “Trận chiến giành Iwo Jima” của tác giả Derrick Wright mà ông vừa nhận được từ một Câu lạc bộ sách lịch sử. Trong khi Bruce đọc, James đã nhảy vào lòng bố để xem tranh vẽ. Khi chờ xem tranh thì James ngồi im nhìn vào trang sách. Thình lình, James chỉ vào một bức tranh của Iwo Jima gần Chichi Jima và nói, “Bố, đó là nơi máy bay của con bị bắn rơi”. Bruce choáng váng.

Vài tuần sau, với những cuộc tìm kiếm nhờ mạng Internet, Bruce đã tới một trang web đề cập đến Hội Natoma Bay. Ông đã liên lạc với Leo Pyatt, người về sau nhận mình đã từng là nhân viên điện đài trên một máy bay chiến đấu Avenger thuộc phi đội VC-81. Bruce không thể cầm lòng, và hỏi Pyatt liệu có chiếc phi cơ Corsair nào đã bay trên Vịnh Natoma không. Pyatt bảo không – chỉ có những chiếc máy bay Avenger và Wildcat thôi. Rồi Bruce hỏi Pyatt có người nào ở đó tên Jack Larsen không. Pyatt bảo ông biết Jack Larsen, nhưng không biết điều gì đã xảy ra với ông ta cả.

Sau khi nhận ra nhiều chi tiết từ đứa con trai 2 tuổi của mình không hiểu vì sao lại hiện thực như vậy, Bruce bị ám ảnh, ông cố gắng bác bỏ bởi vì muốn tin rằng đó chỉ là những “trùng hợp ngẫu nhiên”. Ông bắt đầu lần tìm được những hồ sơ của quân đội từ khắp nước Mỹ. Mục tiêu cuối cùng của ông là để chứng minh việc này không phải là sự thật. Do đó, ông phải tìm Jack Larsen.

Những mảnh câu đố ghép nối thành bức tranh hoàn chỉnh

Bruce không thể tìm được điều gì về Jack Larsen trong các hồ sơ quân đội sau khi con trai họ đề cập đến cái tên ấy. Ông đã tìm kiếm từ mọi danh sách mà ông có thể tìm được từ các Hồ sơ lưu trữ Quốc gia Hoa Kỳ về những người đã chết trong khi phục vụ cho USS Natoma Bay và tất cả các tàu sân bay khác trong suốt Thế chiến II. Có nhiều Larsen và Larson đã hy sinh, nhưng không có Larsen nào ở USS Natoma Bay. Ông đã tìm kiếm hơn một năm, nhưng không có kết quả. Ông suýt nữa đã bỏ cuộc.

Vấn đề là ở chỗ: Bruce đang tìm kiếm một người đã chết. Sau khi dự Cuộc sum họp Vịnh Natoma vào tháng 9 năm 2002, Bruce mới khám phá ra rằng Jack Larsen vẫn còn sống khỏe mạnh tại Springdale, Ark. Sau khi nói chuyện với những cựu quân nhân của chiếc tàu sân bay USS Natoma Bay và gia đình họ, Bruce được biết là có 21 người đã tử trận khi phục vụ cho USS Natoma Bay.

Một trong số những người đó là trung úy James McCready Huston con, thuộc phi đội máy bay chiến đấu VC-81, bị bắn rơi khi mới 21 tuổi trong một nhiệm vụ tấn công đặc biệt vào tàu vận chuyển tại bến cảng Futami Ko ở Chichi Jima, theo như các báo cáo đã được giải mật. Huston đã tình nguyện tham gia vào nhiệm vụ này. Anh là phi công duy nhất của tàu USS Natoma Bay bị bắn rơi tại Chichi Jima.

Đôi vợ chồng nhà Leininger còn nhận ra rằng James đã ký tên mình là “James 3″ trên những bức vẽ chì màu về các máy bay trong Thế chiến II. Cậu thậm chí còn nói mình là “James 3″ – nhiều tháng trước cuộc đoàn tụ ấy – ngụ ý rằng James Huston đã theo tên cha là James, và James Leininger là James thứ 3.

Tới thời điểm đó, Bruce nói ông trở nên nản chí bởi vì nỗ lực chứng minh rằng cậu con trai mình không có tiền kiếp nào cả đang đi nhầm hướng. “Tất cả những bức vẽ của nó đều là máy bay đang chiến đấu, và nó biết chủng loại của những chiếc máy bay. Thậm chí nó còn vẽ cả lá cờ mặt trời đỏ của quân Nhật”, Bruce nói. “Nhưng sau khi nó vẽ “James 3″ lần đầu tiên, tôi mới hỏi nó tại sao lại thế. James nói “Con là thứ 3. Con là James thứ 3″. Nó đã tự gọi mình như thế khi chỉ mới có 3 tuổi. Tôi nghĩ nó đang vật lộn với chuyện gì đó chưa được giải quyết, nếu không thì đã không vẽ mãi những bức tranh ấy…”.

Kiên quyết tìm cho ra ngọn nguồn, Bruce đã tới thăm Larsen ở Akansas vào tháng 9 năm 2002 và hỏi ông về James Huston. Larsen không rõ điều gì đã xảy ra với Huston, nhưng ông chắc chắn là máy bay của Huston đã bị trúng đạn vào ngày 3/3/1945 – cái ngày mà Huston đã không trở về sau nhiệm vụ và vì vậy không rõ là Huston đã chết hay là bị quân địch bắt. Larsen đã là phi công yểm trợ cho Huston trong cái ngày tiến về Chichi Jima ấy.

Sau khi cố gắng kiểm tra các hồ sơ của phi đội VC-81, ông khám phá ra là Huston đã bị bắn rơi trong một chiếc máy bay chiến đấu hiệu FM2 Wildcat chứ không phải là một chiếc Corsair, và không có ai trong Cuộc sum họp đó đề cập gì tới những chiếc máy bay Corsair cất cánh từ USS Natoma Bay. Bruce nói điểm không chính xác đó đã giúp ông nuôi hy vọng rằng tất cả chuyện này chỉ là một chuỗi trùng hợp ngẫu nhiên mà thôi.

Hoài nghi tan biến

Để cho chắc, Bruce cố gắng tìm những thành viên của gia đình Huston. Vào tháng 2/2003 ông đã liên lạc với Anne Huston Baron, là chị của Huston, hiện đang sống tại Los Gatos, California. Qua nhiều cuộc điện đàm, nhà Leininger và bà Barron đã trở thành bạn, và bà đồng ý gửi cho Bruce những hình ảnh của người em trai khi trong quân ngũ. Những gói ảnh đã đến được tay Bruce vào tháng 2 và tháng 3 năm 2003.

Trong một gói ảnh có một bức hình của Huston đang đứng trước một chiếc máy bay chiến đấu Corsair – đúng loại mà James nhắc đi nhắc lại mãi. Theo Bruce, các cuộc phỏng vấn với những thợ bảo dưỡng máy bay và các hồ sơ quân đội đã giải mật, thì trước khi Huston gia nhập USS Natoma Bay và VC-81, anh đã là thành viên của một phi đội ưu tú đặc biệt, là phi đội VF-301 Devil’s Disciples, từ tháng 1 tới tháng 8 năm 1944. Phi đội ưu tú này đã bay thử những chiếc Corsair dùng cho tàu sân bay, và chỉ có 20 phi công được tuyển chọn cho trách nhiệm này. Tuy nhiên, phi đội VF-301 đã bị giải tán sau 8 tháng và Huston được gửi về phi đội VC-81 vào mùng 8/10/1944.

Khi biết được việc này, Bruce nói, tất cả những hoài nghi trong ông đã tan biến. “Tôi không có câu trả lời nào cho việc này, nên tôi cũng không thể giải thích gì cả”, Bruce nói. “Tất cả những giấc mơ có thể là ngẫu nhiên, nhưng có những nhân tố kỳ dị mà bạn buộc phải tính đến. Sét có thể đánh trúng một lần, nhưng khi sét đánh 8 9 lần thì bạn không thể bảo đó là ngẫu nhiên được”.

Bruce đã không kể cho bà Barron về câu chuyện siêu nhiên của đứa con trai cho đến tận tháng 10 năm 2003. Khi cuối cùng ông kể với bà rằng cậu em trai của bà có thể là James, bà nói rằng bà đã choáng. Sau đó, vào ngày 15/10/2003, Bruce và Andrea nhận được một lá thư của bà Barron, cùng với một số đồ đạc cá nhân của Huston. Trong thư bà nói rằng không những là bà cảm thấy James gần gũi, mà còn thực sự tin câu chuyện này.

“Cậu bé không thể biết được những việc này – bé đơn giản là không thể – cho nên tôi tin cậu bé là một phần của em trai tôi”, bà Barron nói. Giờ đây bà gọi cậu bé 6 tuổi là James 3. Và đến lượt mình, cậu cũng xem người phụ nữ 86 tuổi ấy là chị của mình.

Khi Bruce khám phá thêm những thông tin về Huston, vợ chồng nhà Leininger đã tìm thấy những mối liên hệ kỳ lạ khác nữa giữa Huston và con trai của họ. James có 3 búp bê lính Mỹ và đặt tên chúng là Leon, Walter và Billie – đúng tên của 3 phi công bạn của Huston. Theo hồ sơ của Hạm đội Thái Bình Dương Hoa Kỳ, Trung úy Leon Stevens Conner, Thiếu úy Walter John Devlin và Thiếu úy Billie Rufus Peeler nằm trong số 21 người tử trận của USS Natoma Bay. Họ cùng là các thành viên của phi đội máy bay VC-81 với Huston. Bruce hỏi tại sao cậu lại đặt tên cho búp bê như vậy. Cậu bé trả lời: “Bởi vì họ đã chào đón con khi con đến thiên đường”.

Sau khi nghe James nói, Bruce chỉ còn biết rời khỏi phòng trong im lặng sững sờ.

James cũng giải thích cho cha mình rằng máy bay hiệu Corsair thường có lốp phẳng và có xu hướng luôn nghiêng sang trái như thế nào. Sau khi kiểm tra với các nhà sử học quân sự tại Viện bảo tàng Lone Star Flight ở Galveston, Texas, Hoa Kỳ, lời cậu nói đã được xác minh là đúng sự thật. Andrea nhớ lại lần đầu tiên khi cô làm món bánh mì thịt cho James ăn, James đã nói với cô rằng cậu đã không ăn món bánh mì thịt kể từ khi ở Natoma Bay. Vì vậy, Bruce và Andrea liên lạc với một số cựu chiến binh của tàu sân bay USS Natoma Bay, và họ biết được rằng bánh mì thịt là một món ăn chính của phi đoàn.

Ngày máy bay của James Huston bị bắn rơi

Sau khi phát hiện chi tiết về chiếc máy bay Corsair là thật, vẫn còn một điểm cần phải được xác minh: máy bay của Huston bị bắn rơi như thế nào. Có đúng là nó bị hỏa lực phòng không của quân Nhật bắn trúng động cơ, trên vùng trời Iwo Jima như lời James nói hay không?

Tuy nhiên, không ai trong số các phi công yểm trợ của Huston,gồm Jack Larsen, Bob Greenwalt hoặc William Mathson Jr.thuộc phi đội VC-81 đã nhìn thấy máy bay của anh bị bắn rơi vào ngày 03 tháng 3 năm 1945.

Vào tháng 6 năm 2003, một cựu chiến binh khác đã giúp Bruce. Đó là Jack Durham, thành viên của phi đội ném bom và phóng ngư lôi VC-83 của tàu USS Sargent Bay mà đã bay song song với phi đội của Huston vào ngày định mệnh đó. Theo lời Durham, ông đã thấy máy bay của Huston bị bắn hạ bởi hỏa lực phòng không của Nhật. Hơn thế nữa, điều này cũng được xác nhận bởi các báo cáo của phi đội VC-83.

Sau khi nghiên cứu thêm nhiều hồ sơ của phi đội VC-83 và đọc các nhật ký chiến tranh của họ, Bruce đã liên lạc với các thành viên của phi đội VC-83 là Richardson, Bob Skelton và Ralph Clarbour. Tất cả họ đều khẳng định rằng không những máy bay của Huston bị bắn hạ, mà họ còn thấy nó bị trúng đạn ở động cơ, gây ra một tiếng nổ. Clarbour cho biết máy bay của ông đã bay ngay sau chiếc máy bay của James M. Huston Jr. trong cuộc đột kích gần Iwo Jima vào ngày 3/3/1945: “Tôi có thể nói rằng, anh ấy đã bị bắn ngay vào chính giữa động cơ”. Sau đó máy bay của Huston đâm xuống bến cảng Futami Ko, đúng nơi James đã chỉ ra trong cuốn sách lịch sử mà 2 cha con xem vào tháng 11 năm 2000.

Thế là mọi chi tiết các giấc mơ của James đều đã được xác minh là sự thật, và vợ chồng nhà Leininger đã toại nguyện. Thông qua nhiều nhân chứng, nhiều cuộc phỏng vấn cá nhân và các hồ sơ quân đội, Bruce và Andrea tin chắc con trai mình chính là James Huston. Không chỉ có họ, mà nhiều người từng là thân nhân và bạn bè của Huston khi tiếp xúc với James đều đi đến kết luận: James 3 là James Huston đầu thai trở lại.

James tiếp tục nhớ lại những kỷ niệm cuộc đời quá khứ của mình, thậm chí tới tận ngày hôm nay, nhưng tiến sỹ Bowman cho biết trẻ em thường bị mất khả năng nhớ những kỷ niệm về tiền kiếp kể từnăm lên 7. Khi được hỏi tình cảm 2 vợ chồng dành cho đứa con trai có bị ảnh hưởng hay không khi biết nó có thể là một người khác, Bruce trả lời: “Không có gì thay đổi cả. Tôi không nhìn con mình và tự hỏi: “Có phải con trai mình đây không?” Đó là con trai của tôi”.

Cao nguyên Nazca là một trong những bằng chứng về sự hiện hữu của một nền văn minh tiền sử cao cấp, hoàn toàn khác với nền văn minh của chúng ta. Dù đã được nhiều nhà khoa học nghiên cứu nghiêm túc, Nazca vẫn tiếp tục là một trong những “hiện tượng bí ẩn nhất của lịch sử loài người”.

Các đường Nazca là những đường thẳng và hình vẽ lớn bao phủ sa mạc Nazca ở Peru, Nam Mỹ. Các đường kẻ này đã làm các nhà khoa học đau đầu trong suốt nhiều năm qua. Chúng lần đầu tiên được đề cập đến bởi một nhà văn người Tây Ban Nha là Pedro de Cieza de Leon vào năm 1547. Vào những năm 1920, chúng được “tái khám phá” bởi các máy bay bắt đầu bay qua sa mạc này.

Người đầu tiên thực sự nghiên cứu các đường kẻ này là giáo sư Paul Kosok người Mỹ. Năm 1939, Paul Kosock đã dùng một chiếc máy bay nhỏ để quan sát sa mạc Nazca từ trên cao, và ông đã không tin vào mắt mình khi nhìn thấy hình một con chim cách điệu khổng lồ trên sa mạc. Bên cạnh đó là một “tuyến đường” thẳng tắp cắt ngang qua địa hình mấp mô của sa mạc và mất hút ở phía chân trời.

​Sa mạc Nazca là một “cao nguyên cao và khô cằn”, bao phủ hơn 200 dặm vuông. Nhiệt độ khắp cao nguyên này thường giữ ở mức 25 độ C quanh năm, mặc dù vậy nó không dễ chịu gì vì là nơi khô bậc nhất trên thế giới. Sa mạc này có mặt đất màu vàng nhạt, bao phủ bên trên là một lớp sỏi đá giàu oxit sắt màu nâu đỏ. Khi sỏi đá được gỡ bỏ đi, các đường nét sẽ trở nên tương phản rất đậm giữa mặt đất và lớp sỏi đá ấy. Đó là cách mà các hình vẽ nổi bật lên.

Ở đây có nhiều đường thẳng trải dài như vô tận, xuyên qua các đồi núi mà vẫn thẳng nguyên. Còn có nhiều đường thẳng khác nằm song song với nhau, nhiều dạng hình học và tả thực khác có kích thước từ 60 đến gần 300m. Người ta có thể nhận ra hình dáng của một con nhện khổng lồ, một con khỉ có đuôi xoắn ốc, hay hình cá voi, chim, chó, vv… Được chú ý nhiều nhất có lẽ là hình ảnh trên một sườn núi mô tả một người khổng lồ đi giày ống đang giơ tay lên như vẫy chào.

Hình ảnh một con nhện khổng lồ trên sa mạc Nazca​

Con khỉ khổng lồ đuôi xoáy ốc​

Người khổng lồ trên sườn núi đang vẫy tay chào​

Tóm lại, Nazca khiến người ta kinh ngạc vì nhiều điều kỳ lạ:

1) Các hình thù có kích thước lớn, có thể đến 300m, chỉ có thể nhìn thấy được từ trên không. Các nghiên cứu chỉ ra rằng chúng xuất hiện ít nhất cách đây 1500 năm trước, thời mà theo sách giáo khoa và tài liệu lịch sử thì con người hoàn toàn chưa có phương tiện bay nào cho phép quan sát chúng hoặc vẽ nên chúng.

2) Có nhiều đường thẳng dài đến hàng chục km. Có những đường thẳng băng qua các đồi núi mà vẫn giữ nguyên thẳng tắp. Nhiều đường kích thước rất lớn, có thể quan sát được từ vệ tinh.

3) Có những dãy núi rộng lớn bị san bằng một cách hoàn hảo. Trên đó có những đường hình thang khổng lồ trông tựa như những sân bay. Không có dấu vết nào của những người đã tạo ra công trình vĩ đại này. Không tìm thấy bất kỳ công cụ hay thiết bị xây dựng nào, cũng như phần đất đá phần đỉnh đã bị cắt đi của các ngọn núi ấy, ở bất kỳ đâu trong sa mạc Nazca.

Những đường thẳng hoàn hảo, cực dài và cực lớn có thể nhìn thấy được từ vệ tinh, dù đã trải qua hàng ngàn năm phơi trong gió và cát​

Đường thẳng cực dài cắt ngang qua những ngọn đồi phía sau nhưng vẫn thẳng tắp không lệch hướng​

Người “tiền sử” không thể dùng tay và đồ đá để bạt phẳng 1 dãy núi như thế này được. Trong khi chung quanh các dãy núi khác đều còn đỉnh thì riêng dãy núi này các đỉnh núi đã bị san phẳng, trở thành cái mặt bàn cho các hình vẽ sau này. Để san phẳng được cả dãy núi khổng lồ như thế, đến cả công nghệ ngày nay cũng chưa chắc đã làm nổi, nhưng “người tiền sử” từ hàng ngàn hàng vạn năm trước đã làm được​

​Phân tích các giả thuyết

Vào mùa hè năm 2007, một đoàn nghiên cứu quốc tế lớn nhất từ trước đến nay, gồm các nhà khoa học Mỹ, Úc, Đức, Thụy Sĩ và Peru đã đến vùng Nam Mỹ này để xem xét lại toàn bộ các giả thuyết về nguồn gốc của những hình vẽ trên cao nguyên Nazca.

Vào năm 1946, nữ toán học kiêm thiên văn người Đức – Maria Reiche, nhận định rằng, những hình vẽ trên cao nguyên Nazca thể hiện nhận thức về vũ trụ của các bộ lạc sống tại đây từ xa xưa. Ví dụ, họ có thể đã vẽ các chùm sao hay các vật thể khác trên trời, vì hình con nhện tại đây liên tưởng đến tinh vân trong chòm sao Orion, còn hệ thống các đường hình học thì Maria cho rằng đó có thể là lịch của người xưa. Tuy nhiên các nhà khoa học hiện nay đã bác bỏ nhận định trên. Tiến sĩ G.Armin, người Thụy Sĩ thông báo: Ông đã thiết lập bản đồ trắc địa bao gồm 18.000 hình vẽ, sau đó cho vào hệ thống máy vi tính để phân tích, thì không có gì trùng khớp với sự chuyển động của các chòm sao trên trời. G.Armin nói: “Tất cả những gì mà Maria đưa ra chỉ là phỏng đoán mơ hồ, không có căn cứ”.

Cũng có những nhà khoa học đưa ra ý tưởng rằng các bộ lạc nơi này từng sùng bái nước, và dùng các hình vẽ để đánh dấu nơi có thể tìm thấy các nguồn nước sinh hoạt. Tuy nhiên, vào thời đại khi mà những hình vẽ Nazca được tạo ra ít nhất 1500 năm trước thì cao nguyên này có thung lũng trù phú và thổ dân sinh sống, khi đó không bao giờ họ gặp vấn đề khó khăn về nguồn nước, cho nên cũng không có lý do gì để dánh dấu như thế cả.

Vào năm 1955, nhà nghiên cứu người Anh – J.Mozel, đưa ra giả thiết cao nguyên Nazca ngày xưa là sân bay vũ trụ của người ngoài hành tinh và được nhiều người ủng hộ. Nhưng vì sao người ngoài hành tinh lại cần sân bay rộng 500 km2 như thế? Nhiều người cho rằng những thổ dân Nazca trước đây chưa thể có kỹ thuật để vẽ những bức tranh lớn và phức tạp như thế, rằng đó là do người ngoài hành tinh vẽ. Nhưng vào đầu những năm 1980 một nhóm sinh viên và giáo viên đã dùng những chiếc muôi bằng gỗ và trong vòng 14 ngày có thể “vẽ” trên cao nguyên này hình ảnh một con voi lớn mà nhìn từ trên cao không khác các hình cổ. Vì thế giả thiết này cũng không thuyết phục.

Nhà khảo cổ người Đức, trưởng đoàn nghiên cứu quốc tế cho biết: họ đã xem xét, kiểm tra lại các giả thuyết một cách nghiêm túc. Tất cả các giả thuyết đều có lỗ hổng và thiếu thuyết phục. Sau đó họ áp dụng phương pháp loại trừ để suy ra rằng các hình vẽ được sử dụng vào các nghi lễ tôn giáo, rằng người xưa vẽ ra chúng để làm đồ tế lễ dâng cho thần linh để đổi lấy nước mưa, vv… Nhưng tại sao những hình vẽ khổng lồ này chỉ có thể nhìn thấy từ trên không? Theo kết quả khai quật một thành phố cổ nơi đây, các nhà khoa học cho rằng khi đó người Nazca cổ có lẽ đã chế tạo các khinh khí cầu nhỏ có thể bay lên trời trong vòng nửa giờ đồng hồ, nhờ đó quan sát và tạo ra những hình vẽ kỳ lạ này. Tuy nhiên đây cũng chỉ là suy đoán, không có bằng chứng nào cả…

Tất cả các giả thuyết đã biết đều chỉ mới nhằm giải quyết câu hỏi số 1) vì nó có lẽ là dễ trả lời nhất. Như vậy, dẫu miễn cưỡng cho rằng đã có lời giải cho câu đố ấy thì cũng không có ý nghĩa gì, bởi vì bí ẩn thực sự nằm ở 2 câu hỏi hóc búa còn lại đã nêu ở trên. Chúng sẽ mãi mãi là bí ẩn không lời giải đáp, nếu giới khoa học chủ lưu vẫn không dám (hoặc không muốn) nhảy ra khỏi cái khung tư tưởng chật hẹp cũ để tiếp thu nhận thức mới về lịch sử thật của loài người.

Trên thế giới càng ngày càng có nhiều nhà nghiên cứu sau khi khảo cứu vô số tài liệu lịch sử và khảo sát thực địa, đã đi đến kết luận: Cao nguyên Nazca là công trình của một nền văn minh cổ xưa trên trái đất, từng phát triển cực thịnh nhưng đã diệt vong. Nói cụ thể hơn, nó thuộc về nền văn minh vĩ đại mà Plato từng nhắc đến: Atlantis. Vì cao nguyên Nazca là sản phẩm của nền văn minh khác, cho nên phương pháp xây dựng ra nó cũng như mục đích của nó là không thể xác định nếu dùng phương pháp của nền khoa học chúng ta. Hà Đồ, Lạc Thư, Chu Dịch, Bát Quái, Tử Vi Đẩu Số, quả cầu pha lê, kim tự tháp Giza,… cũng đều như vậy. Nền khoa học chúng ta bất quá cũng chỉ tìm hiểu và ứng dụng được chúng ở tầm mức rất hạn chế chứ không thể hiểu thấu đáo được, bởi vì đường lối khoa học của các nền văn minh hoàn toàn khác nhau.

Có lẽ ai cũng biết chuyện khi Christopher Columbus đặt chân lên châu Mỹ vào thế kỷ 16 nhiều người đã nhầm lẫn nơi đây với Ấn Độ và vì thế họ gọi thổ dân da đỏ châu Mỹ là người Anh Điêng. Tuy nhiên còn có nhiều người khác biết rằng lục địa được khám phá chính là Atlantis. Quyển sách đầu tiên đề cập đến điều này là “Lịch sử Ấn Độ và những vùng phụ cận” của Franciso Lopez de Gomara, xuất bản lần đầu năm 1552, bị cấm ngay năm sau đó, và chỉ được tái bản 174 năm sau – tức là năm 1727.

​​Một quyển sách nữa khẳng định rõ ràng Nam Mỹ là Atlantis, là cuốn “Lịch sử của người Incas” do học giả sử gia vĩ đại của thế giới – Sarmiento de Gamboa – viết. Đó là kết quả có được sau một cuộc nghiên cứu chính thức về lịch sử thực sự của người Incas do phó vương Peru thời bấy giờ hậu thuẫn. Quyển sách nói rất rõ rằng Nam Mỹ chính là Atlantis, và vào lúc mà ông đang viết cuốn sách, lục địa này còn được biết đến dưới nhiều cái tên khác nữa là “New Castile” (Castile mới), “New Spain” (Tây Ban Nha mới) hoặc là “Atlanticus”, rồi về sau là “America”. Quyển sách của Sarmiento de Gamboa được gửi tới đức vua Tây Ban Nha thời đó là vua Philip đệ nhị vào năm 1572 và “mất tích” trong hơn 300 năm. Mãi đến năm 1893 nó mới được tìm thấy trong một thư viện ở Đức và được tái bản vào năm 1906.

​​Bản đồ đầu tiên cho biết Nam Mỹ là Atlantis có lẽ là “Bản đồ Tân Thế giới” của Sebastian Muller vẽ vào năm 1540, trong đó ghi rõ “đảo Atlantis”​​

Bản đồ do nhà bản đồ học người Pháp Guillermo Sanson vẽ tại Paris vào năm 1661 nói rõ Nam Mỹ là Atlantis​​

Khu vực Trung Mỹ và Nam Mỹ là nơi tập trung nhiều bất thường các tàn tích kỳ lạ. Người Maya, Kogi, Inca, Olmec,…những quả bóng bằng đá Costa Rica, những hòn đá ICA, thành phố 800m dưới đáy biển Cuba, vv… đều tập trung tại vùng đất này. Người Maya, Kogi, Inca… nói rằng họ là hậu duệ của những người tốt được lựa chọn của một nền văn minh vĩ đại đã diệt vong trong cơn Đại Hồng Thủy, khi đạo đức nhân loại thời kỳ đó đã trở nên bại hoại xấu xa. Nhấn chuột trái vào hình để phóng lớn.​​

Thực ra câu hỏi “Atlantis có thật hay không?” đã có câu trả lời từ lâu. Tại sao phần lịch sử quan trọng bậc nhất ấy lại bị đẩy vào bóng tối để rồi bị lãng quên? Chúng ta cần phải làm gì, khi mà tương lai phụ thuộc vào việc con người hiện tại rút ra được bài học gì từ quá khứ? Chúng ta từ đâu đến và sẽ đi về đâu, điều đó tùy thuộc vào sự lựa chọn của chúng ta.

Theo sách vở hiện tại, Charles Goodyear (1800–1860) là người đã phát minh ra kỹ thuật lưu hóa cao su vào khoảng giữa thế kỷ 19, tức là sau những người bí ẩn tại châu Mỹ gần 3.500 năm.

Người thượng cổ tại Nam Mỹ là những người đầu tiên phát minh ra cao su từ khoảng 3.600 năm trước và đã sử dụng chúng cho nhiều mục đích khác nhau. Đó là kết quả nghiên cứu vào năm 2010 của Học viện Công nghệ Massachusetts.

Các nhà nghiên cứu, giáo sư Dorothy Hosler và Michael Tarkanian thuộc Học viện Công nghệ Massachusetts khẳng định rằng những người cổ xưa đã không chỉ phát minh ra cao su, mà còn hoàn thiện một hệ thống xử lý hóa học để tăng cường các tính chất của cao su.

Có 12 quả bóng cao su đã được tìm thấy tại El Manati và vài địa điểm khảo cổ khác trong khu vực, vào năm 1989, có kích thước từ vài cm đến khoảng 30cm, một số có niên đại lên đến 3.600 năm. Tình trạng bảo tồn nguyên vẹn của chúng chỉ ra rằng những quả bóng này đã trải qua một loại quá trình lưu hóa. Họ cũng khám phá ra rằng các quả bóng đã được làm bằng 2 loại cao su lưu hóa khác nhau.

Sau nhiều cuộc nghiên cứu, các chuyên gia đã kết luận rằng người cổ xưa, để tạo ra các quả bóng cao su ấy đã trộn mủ cao su Panama (Castilla elastica) với nước ép của cây bìm bìm mọc ở những khu vực nhiệt đới tại Trung Mỹ. Loại mủ cao su này ở trạng thái tự nhiên là dạng chất lỏng nhầy dính màu trắng sữa, khi khô rất giòn và không sử dụng được. Cây bìm bìm được nghiền lấy nước và trộn với mủ cao su. Sau khi hỗn hợp cô đặc lại, nó hình thành một khối vật liệu màu trắng và có thể tạo hình được.

Phản ứng hóa học xảy ra khi trộn 2 thứ kể trên lại với nhau đã tạo ra một quá trình lưu hóa cao su tương tự như quá trình lưu hóa cao su hiện đại: Nước ép cây bìm bìm tạo ra các kết nối chéo với các phân tử polymer, khiến cao su đàn hồi và loại bỏ những hợp chất vốn làm cao su giòn yếu.

Có lẽ có 2 kỹ thuật khác nhau được sử dụng để chế tạo những quả bóng này, một là trải cao su ra một bề mặt, phơi khô và cắt thành những mảnh nhỏ, phương pháp thứ 2 là nấu cao su lên rồi nặn thành hình quả bóng.

Bằng cách trộn 2 thành phần trên với các tỉ lệ khác nhau, các nhà nghiên cứu tại Học viện Công nghệ Massachusetts Hoa Kỳ đã khám phá ra rằng: thay đổi thành phần tỉ lệ sẽ cho ra các sản phẩm có đặc tính khác nhau. Tỉ lệ thành phần 50 – 50 cao su và nước ép bìm bìm cho sản phẩm với độ bật nảy tốt nhất, còn tỉ lệ 75 – 25 cho ra sản phẩm có độ bền cao nhất.

Loại cao su bật nảy đàn hồi tốt được dùng cho bóng đá, loại cao su bền chắc và không thấm nước có thể được dùng làm săng-đan như mô tả trong các văn bản Tây Ban Nha thời trung cổ khi họ xâm chiếm châu Mỹ. Một loại vừa bền vừa đàn hồi được dùng rộng rãi để bọc tay cầm cho những cái rìu của họ. Người cổ xưa còn dùng cao su để chế tác những bức tượng rỗng và nhiều vật phẩm khác.

Trong bản báo cáo của Học viện Công nghệ Massachusetts, Giáo sư Tarkanian cho biết tại Nam Mỹ thời bấy giờ đã có “một ngành công nghiệp cao su lớn trong khu vực, sản xuất khoảng 16.000 quả bóng cao su mỗi năm, và nhiều bức tượng, săng-đan, dải băng và các sản phẩm khác”.

Giáo sư Dorothy Hosler còn là chuyên gia nghiên cứu về những kiến thức khoa học cao cấp của các nền văn minh cổ, ví dụ trong lĩnh vực luyện kim. Giáo sư cũng cho biết nhiều thành tựu đáng kinh ngạc của người cổ xưa như bêtông, vữa hồ, và sơn màu… cho đến nay vẫn bị bỏ ngỏ không được nghiên cứu vì những nguyên do bí ẩn.

Theo sách vở hiện tại, Charles Goodyear (1800–1860) là người đã phát minh ra quá trình lưu hóa cao su vào khoảng giữa thế kỷ 19, tức là sau những người bí ẩn tại châu Mỹ gần 3.500 năm.

Hiện vẫn chưa ai biết làm thế nào những người bản địa châu Mỹ cổ đại có được kiến thức ấy: họ đã khám phá nhờ thực nghiệm, do tình cờ, hay là thừa kế từ một nền văn minh nào đó khác?

Charles Berlitz đã ghi chép lại chuyến đi của bác sỹ Ray Brown trong cuốn sách xuất bản năm 1984: “Atlantis: Lục địa thứ 8”. Câu chuyện này cũng góp mặt trong chương trình truyền hình “Tìm kiếm Atlantis”, lần đầu tiên được phát sóng vào năm 1979.

Quả cầu pha lê kỳ lạ

Lời kể của bác sỹ Ray Brown:

Tôi không phải là người đã khám phá ra thành phố cổ đại dưới đáy biển ấy. Chúng tôi nói chuyện với những người khác và họ bảo rằng đã biết về những tàn tích ấy nhiều năm trước đó. Ngay sau khi chúng tôi tới khu vực này, một cơn bão dữ dội ập đến, nên chúng tôi đã ẩn náu xung quanh một trong những hòn đảo gần đó, cho đến khi cơn bão đi qua. Mặc dù chúng tôi đã đánh mất nhiều thiết bị của mình, nhưng chúng tôi vẫn quyết định lặn xuống biển ngay sau khi cơn bão tan.

Lúc ấy làn nước rất tối tăm. Ngay khi chúng tôi tới khu vực này, nơi mà chúng tôi đã trông thấy có thứ gì đó vào năm 1968, chúng tôi đã thấy những tòa nhà, mặc dù trời tối. Chúng tôi chỉ có thể trông thấy hình thù bên ngoài của các kiến trúc. Chúng tôi di chuyển con thuyền hết tới lại lui, và ở bất cứ chỗ nào mà chúng tôi quan sát đều có những kiến trúc ấy. Chúng tôi chọn một chỗ để thả thùng Anke xuống, và trong một trạng thái gần như hoảng sợ, chúng tôi nhảy xuống. Chúng tôi có 5 người lặn, và tôi là người cuối cùng nhảy xuống. Bơi theo từng nhóm 2 người là ý kiến hay, nhất là khi lặn ở những khu vực xa xôi. Lúc nào tôi cũng thấy một cặp chân vịt bơi ở trước mặt mình, và tôi cố gắng bắt kịp họ. Trong một lúc cố gắng, tôi đã bắt kịp, nhưng bị đuối sức, nên dừng lại nghỉ trên một rặng san hô.

Tôi trông thấy ánh sáng vàng kim lấp lánh xuyên qua làn nước tối tăm, và nhận ra rằng ánh sáng phát ra từ một kim tự tháp. Tôi ngồi đó nhìn chằm chằm, đơn giản bởi vì lẽ nào nó lại có thể ở đó được, và tôi ước sao nó đừng biến mất. Ánh sáng phát ra từ phía sau kim tự tháp, tỏa ánh sáng lấp lánh ra các hướng. Cứ như thể ai đó đã vẽ nên bức tranh lộng lẫy này. Tôi nghĩ “Giá như có camera!” thì tôi đã có thể chụp được thời khắc ấy, cảnh tượng vĩ đại nhất trong đời tôi từng thấy, đẹp hơn bất kỳ buổi hoàng hôn nào của thiên nhiên. Một cảnh tượng rực rỡ! Có nhiều màu sắc và cái gì đó rất đẹp xung quanh nó. Ngay khi hoàn hồn, tôi nhận ra rằng cái mà tôi đang trông thấy là bê tông. Nó thực sự tồn tại. Và thay vì chỉ ngồi trên rặng san hô ngắm nhìn nó, tôi đã bơi tới đó. Chỉ có một phần của kim tự tháp ấy nằm ló lên trên lớp cát đáy biển. Tôi có thể thấy được khoảng 30m của nó, căn cứ theo hình thù tôi cho rằng nó giống với một kim tự tháp Ai Cập, và thậm chí có thể còn to hơn. Kim tự tháp này có bề mặt như gương. Nó làm bằng đá, những khối đã láng bóng – một công trình xây dựng xuất sắc phi thường. Những khối đá vỏ ngoài láng bóng ấy được ghép rất khít nhau, đến mức tôi nghĩ cả lưỡi dao cạo cũng không len vào được. Chúng tôi không hiểu làm cách nào người ta có thể đặt những khối đá đẹp đẽ ấy khít nhau đến thế.

Tôi bơi quanh đỉnh của kim tự tháp này. Đang có sóng lớn, nên nguy hiểm nếu ở gần đỉnh, chỗ mà tôi đã bơi quanh lần thứ 3. Trên đường lặn xuống tôi bơi ngang qua một lối vào. Trước đó tôi không thấy lối vào này, và tôi biết chắc là mình đã xem xét kiến trúc này kỹ lưỡng rồi. Tôi không thể giải thích tại sao trước đó lối vào không có ở đó, rồi thình lình nó lại ở đó – Tôi chỉ đang kể cho anh nghe chuyện đó đúng theo những gì tôi nhớ.

​Ý nghĩ đầu tiên của tôi là: Chỗ nào có lối vào, ở đó phải có một cánh cửa. Tôi xem xét rất cẩn thận lần nữa, nhưng không thể tìm thấy cánh cửa nào. Chỉ có lối vào, và không có cửa. Chẳng có gì có thể mở ra được cả. Tôi rất tò mò, và tôi bơi vào bên trong lối vào đó. Tôi băng qua một hành lang nằm ngay bên dưới lối vào, rồi tôi tới một căn phòng rất nguy nga.

Căn phòng này chắc hẳn nằm ở phần bên trên của kim tự tháp. Căn phòng hình chữ nhật, với trần phòng có dạng kim tự tháp. Ở đỉnh chóp của trần phòng có treo một cây gậy kim loại. Cây gậy có bề dày khoảng 8cm và trông giống như vàng, nhưng dường như nó là một thứ kim loại khác chứ không phải vàng. Ở chính giữa phòng có một bệ đá được chạm khắc, bên trên được phủ bằng một tấm kim loại với các cạnh có thể co kéo được. 2 bàn tay kim loại đúng kích thước thật gắn bên trên tấm kim loại, đang giữ một quả cầu pha lê. Cây gậy treo trên đỉnh chóp của trần phòng chỉ thẳng trực tiếp vào quả cầu pha lê đó. Một viên đá màu đỏ bóng láng sắc cạnh gắn chặt vào đầu của cây gậy. Có 7 chiếc ghế rất lớn xung quanh bệ đá, một trong số đó được đặt ở vị trí cao hơn một chút, nó được đặt trên một cái bệ đá của riêng nó.

Tôi bơi lên trần phòng, và chổng ngược đầu đạp chân vào trần phòng, cố nhổ cây gậy khỏi đó. Tôi cảm thấy chắc hẳn rằng đó là vàng. Cây gậy không hề nhúc nhích. Tôi hiểu rằng mình cần có sự giúp đỡ mới lấy được vật báu này. Tôi biết các bạn tôi chỉ còn lại nửa lượng oxy trong bình lặn, và có lẽ họ sẽ không lặn nữa. Vì thế tôi quyết định lấy một thứ gì đó về, để có thể chứng minh với bọn họ điều mà tôi đã nhìn thấy. Tôi lấy dao ra và cố cắt cây gậy, nhưng điều đó chỉ làm lưỡi dao tôi bị hỏng. Mặc dù con dao của tôi làm bằng thứ vật liệu cứng bậc nhất – thép đã tôi. Và không có dấu vết nào trên cây gậy cả!

Tôi bơi trở lại phía những cái ghế và bệ đá, rồi ngồi xuống một trong những cái ghế. Chúng có chỗ gác tay, ngồi rất thoải mái. Sau khi nghỉ một chút, tôi lại bị cuốn hút bởi quả cầu pha lê phát ra ánh sáng rực rỡ. Tôi nhìn quanh phòng, xem liệu có thứ gì lỏng lẻo để tôi có thể mang về được không. Bởi vì lúc ấy tôi chỉ nghĩ “Đây là thực ư? Đẹp quá đi, có thể là một cảnh tượng trong mơ lắm”. Tôi luồn vào giữa đôi bàn tay ấy, và quả cầu pha lê dịch chuyển. Nó không bị gắn chặt! Tôi mang nó về. Đôi bàn tay giữ quả cầu pha lê có màu giống như đồng thau, lòng bàn tay màu vàng kim giống như cây gậy kia. Nhưng nó còn có màu đen, như bị đốt bằng lửa hay bằng một loại năng lượng cao khác. Tôi hơi sợ khi gỡ quả cầu ra khỏi đó. Nếu nó có thể đốt cháy kim loại, thì nó có thể gây ra điều gì đối với tôi? Tôi nắm lấy nó, không có gì xảy ra cả.

Tôi dừng lại một giây, cảm giác rất thanh bình. Và bấy giờ có một giọng nói, khá nặng lời và rất rõ ràng. Nghe như giọng nói vang ra từ chính tòa nhà, từ mọi phía xung quanh tôi. Như là một loại sóng radio nào đó, bảo tôi: “Ông đã đến và có cái mà ông tìm. Giờ thì đi đi và đừng bao giờ quay trở lại nữa”.

Khi tôi trở lại mặt nước và con thuyền, tất cả mọi người trong số chúng tôi đều có trải nghiệm tương tự như thế. Mỗi người đều đã tìm thấy một vài hiện vật và mang một cái về với họ. Một số đồ vật là những thứ trông rất kỳ lạ, có một cái trông giống như cái máy tính điện tử, nhưng không có nút bấm. Chúng tôi chưa bao giờ hiểu được chúng hoạt động như thế nào, hoặc là chúng được dùng để làm gì. Kể từ đó tôi đã có lần lặn ở vùng tam giác Bermuda này, nhưng không bao giờ ở khu vực ấy, tôi không bao giờ muốn quay trở lại nơi ấy nữa.

Bác sỹ Ray Brown

Brown kể rằng “Khắp nơi là các tàn tích và những tòa nhà”, và những người bạn trong nhóm của ông cũng đã trông thấy nhiều tàn tích. “Đối với họ, những tòa nhà ấy trông giống phong cách Ai Cập hoặc cổ điển”. Brown cho biết kim tự tháp đó có phần nổi trên đáy biển cao khoảng 30m, và một phần bị chìm bên dưới lớp cát đáy biển.

Sợ rằng vật báu kỳ lạ của mình có thể bị chính phủ Mỹ tịch thu, bác sỹ Brown không tiết lộ với ai về quả cầu pha lê bí ẩn đó. Mãi cho đến tận năm 1975, lần đầu tiên ông mới cho trưng bày quả cầu pha lê tại một hội nghị chuyên đề tâm linh ở Phoenix.

Kể từ thời điểm đó, quả cầu pha lê chỉ được xuất hiện trước công chúng khoảng 7 lần, nhưng lần nào người ta cũng được trải nghiệm những hiện tượng dị thường mà nó gây ra.

Nếu nhìn chăm chú vào sâu bên trong quả cầu pha lê, người ta thấy được hình ảnh 3 kim tự tháp, cái này xếp sau cái kia kích thước lớn dần. Một số người, trong trạng thái thiền định thâm sâu có thể nhận ra được còn có một kim tự tháp vô hình nữa, nằm chồng lên phía trước 3 kim tự tháp kia.

Brown còn nói dưới những điều kiện nhất định, ta có thể trông thấy một con mắt lớn đang nhìn, và thậm chí hình ảnh của con mắt này đã được chụp, tuy nhiên không được công bố.
Nhà ngoại cảm người Mỹ sống tại New York là bà Elizabeth Bacon khẳng định, trong trạng thái xuất thần, bà được biết rằng quả cầu pha lê này thuộc về Thoth, vị đã chôn giấu một kho tàng kiến thức tại Giza, gần 3 kim tự tháp lừng danh của Ai Cập.

Ánh sáng ảo ảnh, cảm giác gió thổi qua mặc dù phòng kín, sự tồn tại các lớp không khí nóng và lạnh xung quanh quả cầu tại các khoảng cách khác nhau, cảm giác năng lượng, những giọng nói kỳ lạ.

Kim la bàn quay tròn ngược chiều kim đồng hồ khi ở gần quả cầu, nhưng nếu đưa ra bàn xa thêm 5cm nữa kim lại quay tròn theo chiều kim đồng hồ. Khi ở gần quả cầu, các kim loại trở nên có từ tính tạm thời. Quả cầu pha lê có thể đẩy một thanh thép và khiến nó trôi nổi trong không khí, như thể không còn trọng lượng.

Một số người còn khẳng định quả cầu có khả năng chữa bệnh. Một người chạm vào quả cầu có cảm giác được chữa lành, còn người kế tiếp chạm vào cảm giác như thể lâm bệnh thay cho người trước đó.

Cũng như nhiều nhà nghiên cứu và khảo cổ học khác, tiến sỹ Brown tin rằng quả cầu pha lê thuộc về một nền văn minh tồn tại liền trước chu kỳ nhân loại hiện tại, sở hữu những khả năng kỳ lạ mà nhân loại hiện đại chưa hiểu được. Ông nói: “Có thể người xưa hiểu biết hơn chúng ta, về các dạng sống và lực sống, và chúng ta có thể khám phá ra những bí mật của họ”.

Một điều khó hiểu khác nữa, là kể từ sau khi Brown công bố quả cầu pha lê ra công chúng, các thông tin về ông cũng như những người bạn trong chuyến lặn lạ lùng đó đã trở nên rất khó tiếp cận. Có nguồn tin cho biết ông cùng những người khác đã bị buộc phải im lặng, và mọi chi tiết về họ cùng với chuyến đi của họ đều đã bị phong tỏa vì những nguyên do bí ẩn.

Hiện nay quả cầu thuộc về Arthur Fanning, một nhà tâm linh nổi tiếng nước Mỹ.

Thực tế bao giờ cũng lạ lùng hơn tiểu thuyết. Lịch sử thực sự của nhân loại cũng là một thực tế như vậy.

Chúng ta đang sống trong một thời mạt thế, khi mọi giá trị nhân văn của nhân loại đã bị đảo lộn và chà đạp, nơi mà sự thật luôn luôn bị biến thành của riêng cho một số ít người và là món hàng xa xỉ đối với đại chúng. Tuy nhiên, thời đại ấy sắp sửa không còn. Thế giới nhân loại tương lai gần là thời thịnh thế, hòa bình, tươi sáng, nhân ái, hạnh phúc lâu dài, sự thật và lương tâm nhân loại được hồi sinh và tỏa sáng.

Khu vực Trung Mỹ và Nam Mỹ là nơi tập trung nhiều bất thường các tàn tích kỳ lạ. Người Maya, Kogi, Inca, Olmec,… những quả bóng bằng đá Costa Rica, những hòn đá ICA, thành phố 800m dưới đáy biển Cuba, vv… đều tập trung tại vùng đất này. Người Maya, Kogi, Inca đều nói rằng họ là con cháu của một nền văn minh vĩ đại đã diệt vong trong một đại thảm họa toàn cầu. Một số bản đồ thời Trung Cổ ghi Nam Mỹ là Atlantis.

Khổng Tử nói: “Phải nghiên cứu quá khứ nếu muốn xác định được tương lai”. Như vậy, việc hiểu được những bài học then chốt từ lịch sử thực sự của nhân loại sẽ giúp chúng ta tránh được những thảm kịch tương tự sẽ xảy ra đối với loài người.

• Thế giới bị lãng quên: Ai là “Người tiền sử”? (kỳ 1)

 
Pierre Lecomte du Noüy. Cuốn sách “Định mệnh của loài người” của ông thuộc vào hàng best-seller và được đánh giá rất cao.

Tiến sỹ Pierre Lecomte du Noüy (1883-1947) là nhà bác học người Pháp lừng danh thế giới, rất được giới khoa học kính trọng. Ông đạt học vị tiến sỹ trong nhiều ngành khoa học. Có lẽ người ta nhớ đến ông nhiều nhất ở công trình nghiên cứu Vật lý về Sức căng mặt ngoài và các đặc tính khác của chất lỏng.

Ông đã ghi nhận về những nền văn minh xuất hiện vào thời xưa cổ như sau:

“Lịch sử đã cho chúng ta biết về nhiều nền văn minh có trình độ vượt trội nền văn minh của chúng ta hiện nay. Nhưng tất cả chúng đã sụp đổ vào giai đoạn sắp đạt tới mục đích, đời sống đã quá thuận lợi và tuyệt hảo đến độ những kẻ cầm đầu sa vào lối sống nhu nhược và sa đọa, khiến họ mất đi phẩm hạnh và làm họ trở thành những kẻ hèn yếu, dã man, tàn bạo, vô lương tâm, chỉ biết xa hoa trụy lạc… Chính đời sống tiện nghi cực độ sẽ dẫn đến suy vong…”

Khổng Tử nói: “Phải nghiên cứu quá khứ nếu muốn xác định được tương lai”.

Như vậy, việc hiểu được những bài học then chốt từ lịch sử thực sự của nhân loại sẽ giúp chúng ta tránh được những thảm kịch tương tự sẽ xảy ra đối với loài người.

2. Những thanh nối bằng kim loại

Một nét đặc trưng chung khác, được xem là kỹ thuật xây dựng phòng ngừa động đất, là phương tiện dùng để kết nối những khối đá lớn lại với nhau. Nhiều người cho rằng một dạng kim loại nào đó được dùng trong mối nối dạng này. Điều kỳ lạ là chúng cũng xuất hiện ở khắp thế giới cổ xưa.

Ở Angkor Watt (Cambodia)

 
Ở Karnak, và Denderra (Ai Cập)

 
Ở Tiahuanaco (Bolivia), và Ollantaytambo (Peru)

3. Những dấu cắt tách đá

Những nhà xây dựng thời thái cổ đã sử dụng cùng một phương pháp chia tách đá, tại nhiều địa điểm khác nhau trên thế giới. Phương pháp này tương tự với phương pháp mà người hiện đại sử dụng rộng rãi.

Ở Peru, Nam Mỹ

Tại Machu Pichu

Tại Cuzco

Ở Ai Cập

Tại kim tự tháp Menkaure, Giza

Tại Aswan

Tại Châu Âu

  
Tại Carnac, Pháp

  
Tại Castleruddery, Ireland

Tại Bồ Đào Nha

Tại Malta

Tại vùng Chilcas, Mendoza, Argentina. Ảnh: Dario Tursarkisian

Ví dụ đáng chú ý nhất về kỹ thuật tách đá này là dấu tích ở kim tự tháp Yonaguni, nằm dưới đáy biển ở cực nam của Nhật Bản. Nằm dưới đáy đại dương!

4. Những gờ nổi trên các khối đá

Những gờ nổi nhỏ này được tìm thấy tại những công trình xây dựng cổ xưa nhất tại Ai Cập và Nam Mỹ. Chúng có chức năng hay ý nghĩa gì?

Gờ nổi trên khối đá bên trên lối vào “Phòng vua” trong kim tự tháp Lớn Ai Cập

 
Chúng cũng được tìm thấy trên những khối đá granite phủ mặt ngoài của kim tự tháp Menkaure ở Giza.

Những gờ nổi tương tự cũng được tìm thấy tại Osireion, ở Abydoss. Đó là một trong những bằng chứng cho thấy nó cùng thời với “Đền Thung lũng” ở Giza.

Những gờ nổi tương tự cũng được tìm thấy tại các di tích cổ đại ở Nam Mỹ

 
Tại Ollantaytambo, Peru

5. Những khớp nối đá sử dụng mộng

Đáng ngạc nhiên là những khối xây cổ đại của nhiều vùng đất cách rất xa nhau khắp thế giới xưa kia lại cho thấy những hiểu biết tinh vi giống nhau về nhiều loại khớp nối trong đá. Chúng có nhiều nét tương đồng với kỹ thuật mộc của chúng ta ngày nay.

  
Một vài ví dụ về các khớp nối “mộng và lỗ mộng” khác nhau được sử dụng trong The Osirion, ở Abydoss, Ai Cập. Đây được xem là một trong những kiến trúc cổ xưa nhất tại Ai Cập, và chỉ có một kiến trúc cùng thời với nó là “Đền Thung lũng” tại Giza. Cả 2 kiến trúc này đều dùng kỹ thuật kiến trúc trilithon, cũng được thấy tại Stonehenge.

Stonehenge, Anh (khoảng 5.000 năm trước)

Vành đá ngoài cùng ban đầu có 30 khối đá sa thạch được dựng thẳng đứng, mà hiện nay 17 khối vẫn còn đứng vững, mỗi khối nặng khoảng 25 tấn. Đỉnh của những khối đứng này được kết nối bởi một vòng dầm đỡ liên tục nằm ngang bằng đá sa thạch, và chỉ có một phần nhỏ của nó hiện nay vẫn còn nằm nguyên vị trí ban đầu. Những khối đá trong vòng đá sa thạch này được tạo hình cẩn thận và những dầm đỡ ngang này liên kết không chỉ bằng những khớp nối đơn giản, mà chúng còn được khóa chặt bằng các khớp mộng đuôi én phức tạp. Các cạnh được mài nhẵn thành 1 đường cong mềm mại suốt toàn bộ vòng tròn này.

  

Công nghệ chế tác đá tại Tiahuanaco, Peru, Nam Mỹ

Một trong những điều thú vị nhất và kỳ lạ nhất mà di tích này hé lộ, là nhiều khối đá khổng lồ đã được tạo hình như thể chúng là cùng từ một mẫu thiết kế thống nhất, và kinh ngạc thay ăn khớp tinh vi với nhau như bức ảnh bên dưới mô tả. Một lần nữa, những người cổ xưa lại cho chúng ta thấy một bằng chứng buộc nền văn minh chu kỳ này phải suy nghĩ và viết lại lịch sử bị che giấu của loài người. Quy mô công trình và kỹ thuật tinh vi của tàn tích này có thể sánh với các công trình thượng cổ khác tại vùng đất mà ngày nay là Ai Cập.

2 hình trên mô tả sự ghép nối của các khối xây tại Puma-Punku tinh vi như thế nào. Hình dưới mô tả bức tường tại kim tự tháp Akapana với đặc điểm y hệt. Có nhiều ước tính niên đại khác nhau về tàn tích cổ đại tại Puma-Punku, và nhiều người cho rằng các khớp nối trên khoảng 17.000 năm tuổi.

Puma Punku And Tiwanaku With Dr. Robert Schoch

Từ nền văn minh Thung lũng Indus-Sarawati

Từ nền văn minh Thung lũng Indus-Sarawati. Tác phẩm đúc đá (hoặc đá nhân tạo) không thể tin nổi này được tìm thấy ở Harappa, Pakistan, có niên đại ít nhất 4.500 năm trước. Trên bức tượng có nhiều khớp nối sử dụng mộng.

“…Từ xa xưa, loài người đã từng phát triển đến trình độ siêu đẳng. Đó là những xã hội cao cấp, với những tri thức khoa học tinh vi, trải rộng khắp hành tinh. Họ đã xây dựng những công trình kiến trúc vĩ đại như các kim tự tháp, những tòa nhà nguy nga khổng lồ… Nhưng, những điều đó không giúp họ trở nên tốt đẹp và nhân từ hơn, mà trái lại họ ngày càng đắm chìm trong tiện nghi vật chất, trở nên suy đồi và tàn nhẫn, ích kỷ và bệnh hoạn… Những lực lượng cao cấp vô hình rất đau buồn vì điều đó. Họ cảnh báo nhân loại nhiều lần, những mong nhân loại đổi thay, nhưng không có kết quả. Cuối cùng, họ tạo ra đại thảm họa, nhấn chìm và xóa sổ gần như sạch sẽ tất cả dấu vết của thế giới cũ, chỉ có rất ít người tốt được chọn lựa ở mỗi vùng miền trên quả đất là được phù hộ và sống sót. Những người ấy sinh sôi loài người đông trở lại, để rồi, một chu kỳ lịch sử mới lại bắt đầu…”

Vô số phát hiện khảo cổ học đã cho thấy viễn cảnh đó là hoàn toàn có thể.

Đáng chú ý là, có nhiều nét đặc trưng chung trong kỹ thuật xây dựng của các công trình kiến trúc từ thời thượng cổ ở khắp nơi trên thế giới. Sự tương đồng rõ rệt trong thiết kế, kỹ thuật và kỹ năng xây dựng của những chủng người bí ẩn cổ xưa cho thấy một nguồn kiến thức phổ thông của thế giới thời kỳ ấy.

1. Những khối đá gấp góc và những khối đá nhiều mặt

Nhiều kiến trúc thượng cổ cho thấy các khối đá được cắt theo mẫu thiết kế đặc biệt, có tạo hình góc vuông ở đoạn giao 2 bức tường. Nhiều nhà nghiên cứu cho rằng người cổ xưa thiết kế khối xây như vậy để phòng ngừa động đất.

“Đền Thung lũng”, Giza, Ai Cập – Có nhiều khối đá với đặc điểm như vậy tại “Đền Thung lũng”. Khoảng 5.000 năm trước.

Không ai giải thích được tại sao kỹ thuật xây dựng tinh vi như vậy có thể xuất hiện từ 5.000 năm trước. Ở thời điểm đó, theo sách giáo khoa hiện tại, phần đông nhân loại có trình độ thổ dân, sống thành bầy hay bộ lạc, khổ sở hoang dại không hơn súc vật bao nhiêu.

Thổ dân Asmat, Papua, New Guinea, ngày nay.

Nhiều ngàn năm trước….

Luxor, Ai Cập. (trái), Machu Pichu, Peru (phải).

Các khối đá nhiều mặt – Đền Thung lũng, Giza, Ai Cập. Trong khi các khối xây tại Ai Cập thượng cổ đi theo một mặt phẳng nằm ngang, thì các khối xây Nam Mỹ lại có rất nhiều góc cạnh, không theo các mặt phẳng ngang dọc nhất định nào cả. Điều đó đòi hỏi kỹ năng chuyên môn thậm chí còn cao cấp hơn nữa.

Kỹ thuật nề được cho là của người Inca, tại Sacsayhuaman, Cuzco, Nam Mỹ

Sacsayhuaman. Những khối xây khổng lồ, sít chặt nhau đến độ dao lam cũng không len giữa được, có hình dạng và bề mặt không theo quy tắc, khớp chặt với nhau không cần vôi vữa, có khả năng chịu lực rất lớn, chống được động đất. Những con người nhiều ngàn năm trước, chủ nhân của những bức tường kỳ lạ này là ai?

Một trong số 300 bục đá trên đảo Easter. Chúng là những khối đá bazan nặng chừng chục tấn mỗi khối. Kiểu cách của chúng hết sức tương đồng với những khối xây tại Nam Mỹ ở trên.

=> So sánh với công trình kiến trúc của các thổ dân. Theo sách giáo khoa hiện tại, vào thời kỳ các kim tự tháp được xây dựng thì hầu hết chúng ta trông đều giống như thế này:

Nghịch lý ấy là do đâu? Rõ ràng, mô hình lịch sử tuyến tính được dạy trong trường hiện nay không thể giải thích được, không hề thích hợp. Các nhà khoa học dũng cảm hiểu rằng: lịch sử nhân loại cần phải được viết lại từ đầu.

Trông chúng như những bộ phận máy móc hiện đại nào đó. Nhưng thật không ngờ, chúng được làm hoàn toàn bằng đá cứng, từ thời đại mà theo sách giáo khoa phần đông chúng ta vẫn còn đang sống trong hang động.

• Kỹ thuật cơ khí siêu đẳng thời thượng cổ (Kỳ 5)
• Thế giới bị lãng quên: “Người tiền sử” là ai? (kỳ 2)
• Thế giới bị lãng quên: Ai là “Người tiền sử”? (kỳ 1)

Các đồ gia dụng thượng cổ được chế tác bằng máy tiện cơ khí

Trong bảo tàng Cairo và các bảo tàng khác trên thế giới có hàng chục ngàn mẫu vật bằng đá được tìm thấy trong và xung quanh các kim tự tháp bậc thang tại Saqqarra, Ai Cập. Hàng ngàn chiếc bình được cắt gọt từ đá cứng được tìm thấy khắp nơi ở Saqqara, được cho là đã xuất hiện từ những Triều đại đầu tiên (khoảng 6.000 năm trước hoặc hơn). Nhà Ai Cập học số 1 nước Anh, ngài Flinders Petrie cũng tìm thấy những mảnh đồ vật đá tương tự ở Giza. Có một số điều đặc biệt kì dị về những cái bình, bát, lọ và tấm này:

1. Chúng cho thấy các dấu vết đặc trưng của những vật được sản xuất bằng máy tiện. 

2. Nhiều hiện vật được làm từ đá siêu cứng, đòi hỏi những lưỡi cắt siêu cứng để cắt chúng. Phải chăng thiết bị của họ quá siêu việt, cho nên không cần phải quan tâm đến độ cứng của vật liệu? 

3. Nhiều hiện vật khác làm bằng loại đá rất dễ vỡ như đá phiến, nhưng lại có bề mặt mỏng như tờ giấy. 

4. Phần ruột của các hiện vật đá cổ xưa này cho thấy những người bí ẩn ắt phải dùng một thiết bị khoan đặc biệt để cắt gọt chúng. Đáng kinh ngạc thay, phần bên trong cũng được cắt hoàn hảo y hệt phần bên ngoài, gồm cả những phần rất khó như bên dưới vòng cổ của những cái bình. 

5. Việc chế tác có độ khó khăn và độ chính xác rất cao, tuy nhiên chúng đã được sản xuất hàng loạt. Nhiều cái là đồ gia dụng thường ngày. 

6. Những cái bát và đĩa đá được tìm thấy có niên đại từ giai đoạn sớm nhất của nền văn minh Ai Cập, cách nay khoảng 6.000 năm. 

7. Chúng ta không thể tìm được những đồ vật bằng đá như thế này ở bất kỳ thời đại nào sau đó trong lịch sử Ai Cập – có vẻ như các kỹ năng cần thiết đã bị thất truyền.

Chúng được làm từ nhiều loại vật liệu đá khác nhau – từ mềm, chẳng hạn như thạch cao tuyết hoa, cho đến rất cứng, chẳng hạn như đá granite. Làm việc với đá mềm như thạch cao tuyết hoa tương đối đơn giản so với đá granit. Thạch cao tuyết hoa có thể được xử lý bằng các công cụ thô sơ và các chất mài mòn. Còn việc xử lý đá granite là một vấn đề khác hẳn, đòi hỏi không chỉ kỹ năng hoàn hảo, mà còn cả công nghệ khác biệt.

Kỹ thuật của họ thậm chí có thể cao cấp hơn chúng ta. Đây là một trích dẫn của ngài Petrie, nhà Ai Cập học tiên phong hàng đầu của thế giới: “… Máy tiện dường như là một công cụ thường thấy trong Triều đại thứ tư, giống như ở trong các xưởng máy hiện đại ngày nay”. 

Một số những chiếc bình tinh tế này được làm bằng loại đá rất dễ vỡ như đá phiến. Đáng kinh ngạc là chúng còn được tiện và đánh bóng, để tạo ra những góc cạnh và đường cong hoàn mỹ – một thành tích phi thường không tưởng đối với tay nghề thủ công.

Với một mặt đáy nhỏ như vậy – khoảng 3,5 mm vuông – bất kỳ đặc điểm không đối xứng nào cũng sẽ khiến nó không thể đứng thăng bằng được. Loại kỹ năng này đủ để làm kinh ngạc bất kỳ thợ máy nào của thời đại chúng ta. Làm được đối với đồ gốm đã là rất ấn tượng. Nhưng, đối với đá granite thì điều đó là không thể tin nổi.

 

Không chỉ có một số ít những hiện vật như thế. Có đến hàng ngàn đồ tạo tác dạng này trong và xung quanh kim tự tháp Step, Ai Cập. Nhiều hiện vật bằng đá này đã được tìm thấy tại đây. Nhiều đồ tạo tác đã bị khắc những biểu tượng của các vị vua đầu tiên của Ai Cập – các quốc vương thời kỳ tiền Vương triều – từ trước cả thời kỳ của các pharaông, khoảng 6.000 năm trước đây. Căn cứ theo kiểu dáng và kỹ năng các chữ khắc này, có vẻ các hiện vật ấy không phải thuộc thời kỳ tiền vương triều Ai Cập, mà có nhiều khả năng là các chữ khắc đã được khắc thêm vào sau khi những người thuộc thời kỳ đó tìm thấy chúng. Thế thì, những người đã chế tác ra các hiện vật này là ai? Họ đã chế tác chúng bằng cách nào, ở đâu, và khi nào? Và tại sao những vật dụng gia đình thường nhật của họ lại bị chôn vùi trong các kim tự tháp Ai Cập cổ xưa nhất?  

Một vài mẫu vật không tưởng khác 

Tốc độ cắt của các thiết bị khoan hiện đại, nhà khoa học Chris Dunn tính toán được là 0,0005cm/vòng quay. Như vậy những người bí ẩn ở vùng đất Ai Cập ấy đã khoan vào đá granite với tốc độ khoan lớn hơn 500 lần so với các máy khoan hiện đại.

Kỹ thuật khoan lấy lõi thời cổ đại

Để tạo ra những lỗ khoan lõi kiểu như vậy, rõ rằng cần phải có khai thác mỏ và luyện kim, sự chế tạo các mũi khoan, kinh nghiệm sử dụng vật liệu mài, kỹ thuật xoay tròn – bánh xe, và tất cả những thứ có liên quan với nó. Nhiều nhà khoa học cho rằng những lỗ khoan này là do người hiện đại thực hiện. Tuy nhiên, những ý kiến này không được chấp nhận bởi theo các ghi chép lịch sử thì 1000 năm trước, đã có các văn bản miêu tả về những lỗ khoan bao tâm vô cùng bí ẩn này.

Vậy thì, những người sống trên vùng đất Ai Cập thời thái cổ làm thế nào tạo ra được các lỗ khoan nhẵn nhụi và tròn trịa đến như thế, nếu thời họ sống chưa phát minh ra kỹ thuật khoan bao tâm, và các công cụ đều làm bằng đồng? Nhà Ai Cập học vĩ đại, sir Flinder Petrie cũng khẳng định rằng những người tiền Ai Cập cổ đã sử dụng máy khoan trong một số công trình và tác phẩm của họ. Phương pháp khoan lõi đã được những người tại vùng đất Ai Cập thượng cổ sử dụng rất rộng rãi để chế tác đá cứng, nhiều khi chỉ để loại bỏ phần đá thừa trong các tác phẩm của họ. Điều đó chứng tỏ kỹ thuật khoan cơ khí này là rất dễ dàng đối với chủng người bí ẩn ấy. 

Tốc độ khoan 500 lần nhanh hơn máy khoan hiện đại 

Khi xem xét kỹ các vết khoan để lại, rõ ràng thiết bị khoan bí ẩn ấy đã sử dụng một áp lực lớn ép xuống dưới. Khoảng cách giữa các rãnh khoan có thể được sử dụng để đo độ lớn của áp lực đã được áp dụng. Petrie nói về điều này như sau: “Trên lõi đá granit, mẫu vật số 7, rãnh xoắn ốc của vết cắt tiến vào dần với tốc độ 0,25cm trong một tiết diện có chu vi 15cm, nghĩa là 1/60, là một tốc độ cắt thạch anh và fenspat đáng kinh ngạc”. Tốc độ cắt của các thiết bị khoan hiện đại, nhà khoa học Chris Dunn tính toán được là 0,0005cm/vòng quay, cho thấy những người bí ẩn ở vùng đất Ai Cập ấy đã khoan vào đá granite với tốc độ khoan nhanh hơn 500 lần so với các máy khoan hiện đại.

Lỗ khoan bao tâm trong đá granite hồng, được tìm thấy tại “Đền thung lũng” Ai Cập. “Đền thung lũng” cùng với các kim tự tháp Giza có nhiều điểm khác biệt so với phần còn lại của Ai Cập cổ đại, cho thấy trình độ công nghệ cao hơn hẳn.

Phần lõi đá của lỗ khoan bao tâm. Đá granite hồng. Được ngài William Flinders Petrie tìm thấy vào năm 1881.

“Những khoan hình ống này có độ dày khác nhau, có đường kính từ 6mm đến 13cm và dày từ 0,8mm đến 5mm. Lỗ khoan nhỏ nhất được tìm thấy trong đá granite có đường kính 5cm”. “…Còn có một mẫu lớn hơn, ở nơi mà một cái nền đá vôi đã được đẽo gọt, bằng cách cắt nó ra bằng những ống khoan có đường kính khoảng 46cm; các rãnh tròn đôi khi giao nhau, chứng minh rằng nó đã được thực hiện chỉ đơn thuần là để loại bỏ phần đá thừa đó”.

Ngài W.M. Flinders Petrie, nhà Ai Cập học số 1 Anh quốc, 1883

Các dấu khoan trong lòng đá cứng khắp thế giới cổ xưa

Morbihan, Pháp. 3 ảnh liền trên là những phiến đá với những dấu khoan trên bề mặt. Dấu khoan trên các phiến đá song song với nhau, cho thấy các tảng đá lớn đã được khoan để tách làm đôi.

Mnajdra, Malta. Hằng trăm lỗ khoan trang trí trên những khối đá. Có niên đại khoảng 6.000 năm.

Tiahuanaco. Kiểm tra kỹ lưỡng khối đá trên, người ta thấy những dấu khoan cách đều nhau dọc theo chiều dài của vết cắt chính xác rộng 6mm này.